题目内容
5.不等式($\frac{1}{2}$-x)($\frac{1}{3}$-x)>0的解集是( )| A. | {x|$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x>$\frac{1}{2}$} | C. | {x|x<$\frac{1}{3}$} | D. | {x|x<$\frac{1}{3}$或x>$\frac{1}{2}$} |
分析 不等式化为(x-$\frac{1}{2}$)(x-$\frac{1}{3}$)>0,求出解集即可.
解答 解:不等式($\frac{1}{2}$-x)($\frac{1}{3}$-x)>0
化为(x-$\frac{1}{2}$)(x-$\frac{1}{3}$)>0,
解得x<$\frac{1}{3}$或x>$\frac{1}{2}$,
∴不等式的解集是{x|x<$\frac{1}{3}$或x>$\frac{1}{2}$}.
故选:D.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
20.集合A={x|x2-4=0}的子集个数( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
17.已知tanα,$\frac{1}{tanα}$是关于x的方程x2-kx+k2-3=0的两个实根,且3π<α<$\frac{7}{2}$π,则cosα+sinα=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
 四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD
四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD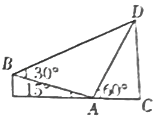 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.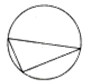 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)