题目内容
9.已知数列{an}前n项和为Sn,且Sn=2an-(n-1)q-1,其中n∈N*,q为常数.(Ⅰ)当q=0时,求数列{an}的通项公式;
(Ⅱ)当q>1时,对任意n∈N*,且n≥2,证明:$\frac{1}{1+{a}_{1}}$+$\frac{1}{1+{a}_{2}}$+$\frac{1}{1+{a}_{3}}$+…+$\frac{1}{1+{a}_{n}}$<1.
分析 (Ⅰ)∵Sn=2an-(n-1)q-1…①,当n≥2时,Sn-1=2an-1-(n-2)q-1…②
①-②得an=2(an-an-1)-q⇒an=2an-1+q.
故当q=0时,$\frac{{a}_{n}}{{a}_{n-1}}=2\\;(n≥2)$,即数列{an}是首项为1,公比为2的等比数列.
(Ⅱ)由(Ⅰ)得an=2an-1+q.,a1=1.当q>1时,an=2an-1+q.>2an-1+1,
即$\frac{{a}_{n}+1}{{a}_{n-1}+1}>2\\;\\;(n≥2)$,${a}_{n}+1>{2}^{n}$,$\frac{1}{{a}_{n}+1}<\frac{1}{{2}^{n}}$.
可得$\frac{1}{1+{a}_{1}}$+$\frac{1}{1+{a}_{2}}$+$\frac{1}{1+{a}_{3}}$+…+$\frac{1}{1+{a}_{n}}$<$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$<1.
解答 解:(Ⅰ)∵Sn=2an-(n-1)q-1…①,
∴当n≥2时,Sn-1=2an-1-(n-2)q-1…②
①-②得an=2(an-an-1)-q⇒an=2an-1+q.
故当q=0时,$\frac{{a}_{n}}{{a}_{n-1}}=2\\;(n≥2)$,a1=s1=2a1-1,∴a1=1.
即数列{an}是首项为1,公比为2的等比数列,∴${a}_{n}={2}^{n-1}$;
(Ⅱ)证明:由(Ⅰ)得an=2an-1+q.,a1=1.
当q>1时,an=2an-1+q>2an-1+1,
即$\frac{{a}_{n}+1}{{a}_{n-1}+1}>2\\;\\;(n≥2)$
∴$\frac{{a}_{2}+1}{{a}_{1}+1}•\frac{{a}_{3}+1}{{a}_{2}+1}•\frac{{a}_{4}+1}{{a}_{3}+1}…\frac{{a}_{n}+1}{{a}_{n-1}+1}$>2n-1
∴${a}_{n}+1>{2}^{n}$,$\frac{1}{{a}_{n}+1}<\frac{1}{{2}^{n}}$.
则:$\frac{1}{1+{a}_{1}}$+$\frac{1}{1+{a}_{2}}$+$\frac{1}{1+{a}_{3}}$+…+$\frac{1}{1+{a}_{n}}$<$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$<1.
∴$\frac{1}{1+{a}_{1}}$+$\frac{1}{1+{a}_{2}}$+$\frac{1}{1+{a}_{3}}$+…+$\frac{1}{1+{a}_{n}}$<1
点评 本题考查了利用数列的递推式求通项、数列中的放缩法,属于难题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
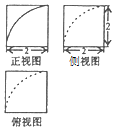
| A. | 24+π | B. | 24-3π | C. | 24-π | D. | 24-2π |
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
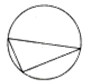 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)