题目内容
4.已知函数f(x)=x2-2x+mlnx(m∈R),$g(x)=(x-\frac{3}{4}){e^x}$.(Ⅰ)若m=1,求y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若f(x)存在两个极值点x1,x2(x1<x2),求g(x1-x2)的最小值.
分析 (Ⅰ)求出函数的导数,求出k的值,求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;
(Ⅲ)求出${x_1}=\frac{{1-\sqrt{1-2m}}}{2},{x_2}=\frac{{1+\sqrt{1-2m}}}{2}$,${x_1}-{x_2}=-\sqrt{1-2m}$,令$t=-\sqrt{1-2m}(m∈(0,\frac{1}{2})),t∈(-1,0)$,则问题转化为$g(t)=(t-\frac{3}{4}){e^t}$在$t∈(0,\frac{1}{2})$的最值,根据函数的单调性求出其最小值即可.
解答 解:(Ⅰ)m=1时,f(x)=x2-2x+lnx
所以${f^/}(x)=2x-2+\frac{1}{x}=\frac{{2{x^2}-2x+1}}{x}(x>0)⇒{f^/}(1)=1,k=1$,∵f(1)=-1,
所以在点(1,f(1))处的切线方程为y+1=k(x-1)=x-1⇒x-y-2=0…(3分)
(Ⅱ)${f^/}(x)=2x-2+\frac{m}{x}=\frac{{2{x^2}-2x+m}}{x}(x>0)$
∵2x2-2x+m=0的△=4-8m的对称轴为$x=\frac{1}{2}$…(5分)
(1)当△<0即$m>\frac{1}{2}$时,方程2x2-2x+m=0无解,
${f^/}(x)=2x-2+\frac{m}{x}=\frac{{2{x^2}-2x+m}}{x}≥0$在(0,+∞)恒成立,
所以f(x)在(0,+∞)单增
当△=0即$m=\frac{1}{2}$时,方程2x2-2x+m=0有相等的实数解,…(6分)
${f^/}(x)=2x-2+\frac{m}{x}=\frac{{2{x^2}-2x+m}}{x}≥0$在(0,+∞)恒成立,
所以f(x)在(0,+∞)单增;
(2)当△>0即$m<\frac{1}{2}$时,方程2x2-2x+m=0有解,
解得${x_1}=\frac{{1-\sqrt{1-2m}}}{2},{x_2}=\frac{{1+\sqrt{1-2m}}}{2}$
当m≤0时,x1<0<x2,解不等式${f^/}(x)=2x-2+\frac{m}{x}=\frac{{2{x^2}-2x+m}}{x}>0⇒x>{x_2}$
所以f(x)在(x2,+∞)单增,在(0,x2)单减;
当$0<m<\frac{1}{2}$时,0<x1<x2,解不等式$\frac{{2{x^2}-2x+m}}{x}>0⇒x>{x_2}或0<x<{x_1}$
所以f(x)在(x2,+∞)单增,在(x1,x2)单减,在(x2,+∞)和(0,x1)单增,…(8分)
综上所得:m≤0时,函数在(0,$\frac{1+\sqrt{1-2m}}{2}$)单调递减,($\frac{1+\sqrt{1-2m}}{2}$,+∞)单调递增;
0<m<$\frac{1}{2}$时,函数在(0,$\frac{1-\sqrt{1-2m}}{2}$)单调递增,在($\frac{1-\sqrt{1-2m}}{2}$,$\frac{1+\sqrt{1-2m}}{2}$)单调递减,($\frac{1+\sqrt{1-2m}}{2}$,+∞)单调递增;
m≥$\frac{1}{2}$时,函数在(0,+∞)单调递增 …(9分)
(Ⅲ)?由(Ⅰ)可知当$m∈(0,\frac{1}{2})$时函数f(x)有两个极值点x1,x2,(x1<x2),
且x1,x2为方程2x2-2x+m=0的两个根,
则${x_1}=\frac{{1-\sqrt{1-2m}}}{2},{x_2}=\frac{{1+\sqrt{1-2m}}}{2}$,${x_1}-{x_2}=-\sqrt{1-2m}$,
令$t=-\sqrt{1-2m}(m∈(0,\frac{1}{2})),t∈(-1,0)$,
则问题转化为$g(t)=(t-\frac{3}{4}){e^t}$在$t∈(0,\frac{1}{2})$的最值,
又∵${g^/}(t)=(t-\frac{3}{4}){e^t}+{e^t}=(t+\frac{1}{4}){e^t}$,且$t∈(-1,-\frac{1}{4})时{g^/}(t)≤0,t∈[{-\frac{1}{4},0})时{g^/}(t)≥0$,
…(11分)
所以g(t)在$t∈(-1,-\frac{1}{4})时g(t)单减,t∈[{-\frac{1}{4},0})时g(t)单增$,
所以当$t=-\frac{1}{4}$时g(t)最小.
∴$g{(t)_{min}}=g(-\frac{1}{4})=-{e^{-\frac{1}{4}}}$…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,考查切线方程问题,是一道综合题.

| A. | 0 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{9}{8}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
 四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD
四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD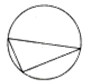 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)