题目内容
2.已知函数f(x)(x∈R)的导函数为f′(x),满足f(3)=7,f′(x)<2,则f(x)<2x+1的解集为(3,+∞).分析 由f′(x)<2,则f(x)<2x+1可抽象出一个新函数g(x),利用新函数的性质(单调性)解决问题,即可得到答案.
解答 解:设g(x)=f(x)-(2x+1),
因为f(3)=7,f′(x)<2,
所以g(3)=f(3)-(2×3+1)=0,
g′(x)=f′(x)-2<0,
所以g(x)在R上是减函数,且g(3)=0.
所以f(x)<2x+1的解集即是g(x)<0=g(3)的解集.
所以x>3.
故答案为:(3,+∞).
点评 本题考查利用导数研究函数的单调性,解决此类问题的关键是构造函数g(x)=f(x)-(2x+1),然后利用导数研究g(x)的单调性,从而解决问题,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.已知i为虚数单位,则复数$\frac{1-i}{1+i}$的模为( )
| A. | 0 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
17.已知tanα,$\frac{1}{tanα}$是关于x的方程x2-kx+k2-3=0的两个实根,且3π<α<$\frac{7}{2}$π,则cosα+sinα=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
7.已知U={x∈N|x<6},P={2,4},Q={1,3,4,6},则(∁UP)∩Q=( )
| A. | {3,4} | B. | {3,6} | C. | {1,3} | D. | {1,4} |
7.已知i是虚数单位,则i+|i|在复平面上对应的点是( )
| A. | (1,0) | B. | (0,1) | C. | (1,1) | D. | (1,-1) |
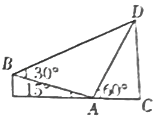 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.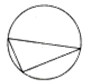 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)