题目内容
19.已知角θ的终边过点P(-12,5),求sinθ,cosθ,tanθ三角函数值.分析 由题意利用任意角的三角函数的定义,求得sinθ,cosθ,tanθ三角函数值.
解答 解:(1)∵角θ的终边过点P(-12,5),∴x=-12,y=5,r=|OP|=13,
∴sinθ=$\frac{y}{r}$=$\frac{5}{13}$,cosθ=$\frac{x}{r}$=-$\frac{12}{13}$,tanθ=$\frac{y}{x}$=-$\frac{5}{12}$.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
相关题目
9.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$右焦点为F,过F作与x轴垂直的直线l与两条渐近线相交于A、B两点,P是直线l与双曲线的一个交点.设O为坐标原点.若有实数m、n,使得$\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$,且$mn=\frac{2}{9}$,则该双曲线的离心率为( )
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{9}{8}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
7.已知U={x∈N|x<6},P={2,4},Q={1,3,4,6},则(∁UP)∩Q=( )
| A. | {3,4} | B. | {3,6} | C. | {1,3} | D. | {1,4} |
7.已知i是虚数单位,则i+|i|在复平面上对应的点是( )
| A. | (1,0) | B. | (0,1) | C. | (1,1) | D. | (1,-1) |
4.设a=$\frac{\sqrt{2}}{2}$(sin 17°+cos 17°),b=2cos213°-1,c=sin 37°•sin 67°+sin 53°sin 23°,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | b<a<c |
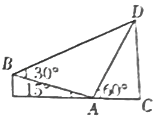 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.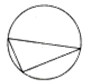 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)