题目内容
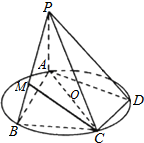 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=| 3 |
| 1 |
| 3 |
(1)求证:CM∥平面PAD;
(2)求异面直线BP与CD所成角的余弦值.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)作ME⊥AB于E,连接CE,则ME∥AB由圆的性质得EC∥AD,从而平面MEC∥平面PAD,由此能证明CM∥平面PAD.
(2)过点A作平行于BC的直线交CD的延长线于G,作BF∥CG,连接PF,∠PBF为异面直线BP与CD所成角,由此能求出异面直线BP与CD所成角的余弦值.
(2)过点A作平行于BC的直线交CD的延长线于G,作BF∥CG,连接PF,∠PBF为异面直线BP与CD所成角,由此能求出异面直线BP与CD所成角的余弦值.
解答:
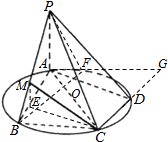 (1)证明:作ME⊥AB于E,连接CE,∴CE⊥AP,…①
(1)证明:作ME⊥AB于E,连接CE,∴CE⊥AP,…①
∵AC是圆O的直径,AC=2BC=2CD=2,
∴AD⊥DC,AB⊥BC,∴∠BAC=∠CAD=30°,
∠BCA=∠DCA=60°,AB=AD=
,
BM=
BP,∴BE=
BA=
,tan∠BCE=
,
∴∠BCE=∠ECA=30°=∠CAD,
∴EC∥AD,…②
又ME∩CE=E,PA∩DA=A,
∴平面MEC∥平面PAD,CM?平面MEC,CM?平面PAD,
∴CM∥平面PAD.
(2)解:过点A作平行于BC的直线交CD的延长线于G,
作BF∥CG,连接PF,
则∠PBF为异面直线BP与CD所成角,设∠PBF=θ,
AF=1,PB=
,BF=2,PF=2,
∴cosθ=
=
=
.
 (1)证明:作ME⊥AB于E,连接CE,∴CE⊥AP,…①
(1)证明:作ME⊥AB于E,连接CE,∴CE⊥AP,…①∵AC是圆O的直径,AC=2BC=2CD=2,
∴AD⊥DC,AB⊥BC,∴∠BAC=∠CAD=30°,
∠BCA=∠DCA=60°,AB=AD=
| 3 |
BM=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
∴∠BCE=∠ECA=30°=∠CAD,
∴EC∥AD,…②
又ME∩CE=E,PA∩DA=A,
∴平面MEC∥平面PAD,CM?平面MEC,CM?平面PAD,
∴CM∥平面PAD.
(2)解:过点A作平行于BC的直线交CD的延长线于G,
作BF∥CG,连接PF,
则∠PBF为异面直线BP与CD所成角,设∠PBF=θ,
AF=1,PB=
| 6 |
∴cosθ=
| PB2+BF2-PF2 |
| 2PB•BF |
| 6+4-4 | ||
2
|
| ||
| 4 |
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列命题中错误的是( )
| A、命题“?x∈R,x2+1≥0”的否定是:?x∈R,x2+1<0 |
| B、在△ABC中,“sinA>sinB”是“∠A>∠B”的充要条件 |
| C、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| D、若命题p:?x∈R,tanx=1,命题q:?x∈R,x2-x+1>0,则命题“p∧q”是假命题 |