题目内容
春节后购物旺季随之转向淡季,商家均用各种方法促销,某商场规定:凡购物均可获得一次抽奖机会,抽奖方法为:编号1~10的相同小球中任意有放回地抽一个小球,若抽到编号为6或8的小球则再获一次机会,最多抽取三次.
(1)求顾客恰有两次抽奖机会的概率;
(2)规定:一等奖为号码含3个6,奖金5000元;二等奖为号码含2个6,奖金1000元,顾客抽得号码只能兑最高奖一次,求顾客购物一次获奖金额的分布列及数学期望.
(1)求顾客恰有两次抽奖机会的概率;
(2)规定:一等奖为号码含3个6,奖金5000元;二等奖为号码含2个6,奖金1000元,顾客抽得号码只能兑最高奖一次,求顾客购物一次获奖金额的分布列及数学期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)设事件A=“顾客恰有两次抽奖机会”,利用相互独立事件概率乘法公式能求出顾客恰有两次抽奖机会的概率.
(2)记顾客购物一次获奖金额为随机变量ξ,则ξ的可能取值为5000,1000,0,由此能求出ξ的分布列和Eξ.
(2)记顾客购物一次获奖金额为随机变量ξ,则ξ的可能取值为5000,1000,0,由此能求出ξ的分布列和Eξ.
解答:
解:(1)设事件A=“顾客恰有两次抽奖机会”,
则P(A)=
×
=
.
(2)记顾客购物一次获奖金额为随机变量ξ,则ξ的可能取值为5000,1000,0,
根据题意有:
P(ξ=5000)=
×
×
=
,
P(ξ=1000)=
×
×
+
×
×
+
×
×
=
,
P(ξ=0)=1-P(ξ=5000)-P(ξ=1000)=
,
∴ξ的分布列为:
∴Eξ=5000×
+1000×
+0×
=16.
则P(A)=
| 2 |
| 10 |
| 8 |
| 10 |
| 4 |
| 25 |
(2)记顾客购物一次获奖金额为随机变量ξ,则ξ的可能取值为5000,1000,0,
根据题意有:
P(ξ=5000)=
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 1000 |
P(ξ=1000)=
| 1 |
| 10 |
| 1 |
| 10 |
| 9 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 11 |
| 1000 |
P(ξ=0)=1-P(ξ=5000)-P(ξ=1000)=
| 988 |
| 1000 |
∴ξ的分布列为:
| ξ | 5000 | 1000 | 0 | ||||||
| P |
|
|
|
| 1 |
| 1000 |
| 11 |
| 1000 |
| 988 |
| 1000 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
相关题目
若条件p:|x|≤2,条件q:x≤a,且p是q的充分不必要条件,则a的取值范围是( )
| A、a≥2 | B、a≤2 |
| C、a≥-2 | D、a≤-2 |
设复数z1,z2在复平面内对应的点关于虚轴对称,若z1=1-2i,则
的虚部为( )
| z2 |
| z1 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
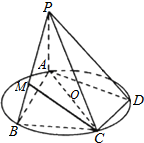 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=