题目内容
设A={x|x2-4x-5=0},B={x|x2=1},求A∪B,A∩B.
考点:交集及其运算,并集及其运算
专题:集合
分析:利用二次函数的性质求出A={x|x2-4x-5=0}={-1,5},B={x|x2=1}={-1,1},由此能求出A∪B和A∩B.
解答:
解:∵A={x|x2-4x-5=0}={-1,5},B={x|x2=1}={-1,1},
∴A∪B={-1,1,5},A∩B={-1}.
∴A∪B={-1,1,5},A∩B={-1}.
点评:本题考查并集和交集的求法,是基础题,解题时要注意二次函数的性质的合理运用.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
对任意实数k,直线y=kx+1与圆x2+y2=4的位置关系一定是( )
| A、相离 | B、相切 |
| C、相交且不过圆心 | D、相交且过圆心 |
函数f(x)=2x+2x-3的零点所在的大致区间是( )
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,3) |
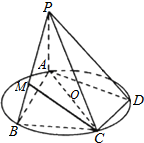 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=