题目内容

若点（x，y）位于曲线y=|x-2|与y=1所围成的封闭区域内，则2x+y的最小值为
 
．
考点：简单线性规划
专题：不等式的解法及应用
分析：设z=2x+y，由z=2x+y得y=-2x+z，然后平移直线，利用z的几何意义确定目标函数的最小值即可．
解答： 解：作出平面区域如图：
设z=2x+y，由z=2x+y得y=-2x+z，
平移直线y=-2x+z，则由图象可知当直线经过点A时，
直线y=-2x+z的截距最小，此时z最小．
由
y=2-x
y=1
，解得
x=1
y=1
，即A（1，1）代入目标函数z=2x+y得z=2×1+1=3．
故答案为：3．
点评：本题主要考查线性规划的基本应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
数列{an}中，a1=3，a2=6，an+2=an+1-an，那么a6=（　　）
A、-2B、-3C、-6D、-8
已知函数f（x）=ex，g（x）=ax2（a∈R，a≠0）．
（1）求函数y=
g(x)
f(x)
的单调区间；
（2）①已知A（x1，y1），B（x2，y2）（x1＜x2）为函数y=g（x）图象上的两点，y=g′（x）为y=g（x）的导函数，若g′（x0）=
y1-y2
x1-x2
，求证：x0∈（x1，x2）；
②类比函数y=g（x），①中的结论在函数y=f（x）中是否成立？若成立，请给出证明；若不成立，请说明理由．
已知f（x）=cos（2x+
π
3
）+1-2cos2x．
（1）求函数f（x）的单调递减区间；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，且a=1，b+c=2，f（A）=-
1
2
，求△ABC的面积．
由两个四棱锥组合而成的空间几何体的三视图如图所示，其体积是
 
；表面积是
 
．
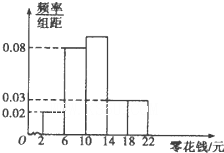为了引导学生树立正确的消费观，某校调查了全校1000名学生每天零花钱的数量，绘制频率分布直方图如图，则每天的零花钱数量在[6，14）内的学生人数为
 
．
y=
3x+1
x+2
的渐近线方程为
 
．
设变量x，y满足
x-2y+2≥0
x+y-2≥0
x≤3
，则z=2x-y的最大值为
 
．
已知（1+2x）8展开式的二项式系数的最大值为a，系数的最大值为b，则
b
a
=（　　）
A、
128
5
B、
256
7
C、
512
5
D、
128
7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网