题目内容
已知a>0,函数f(x)=
x3-ax2+x+1.
(Ⅰ)若f(x)在x=x1,x=x2处取得极值,且1<
≤5,求实数a的取值范围;
(Ⅱ)当x≥2时,求3f(x)+|f′(a)-1|的最小值.
| a |
| 3 |
(Ⅰ)若f(x)在x=x1,x=x2处取得极值,且1<
| x2 |
| x1 |
(Ⅱ)当x≥2时,求3f(x)+|f′(a)-1|的最小值.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)利用求函数极值的方法,和根与系数的关系,得出参数a的范围.
(Ⅱ)首先判断f(x)单调递增函数,求出f(x)的最小值,令g(a)=3f(x)+|f'(a)-1|,问题得以解决.
(Ⅱ)首先判断f(x)单调递增函数,求出f(x)的最小值,令g(a)=3f(x)+|f'(a)-1|,问题得以解决.
解答:
解(Ⅰ) f'(x)=ax2-2ax+1.
∵x1,x2是f(x)的两个极值点,所以x1,x2是f'(x)=0的两根.
∴x1+x2=2,x1•x2=
.
又∵1<
≤5,
∴2<
≤6.
∴1<
≤3.
从而
≤x1<1.
∴
=x1x2=x1(2-x1)=-(x1-1)2+1
当
≤x1<1时,
∈[
,1).
故 a∈(1,
].
(Ⅱ)当x≥2时,f'(x)单调递增
∴f'(x)≥f'(2)=1.
∴f(x)单调递增
∴f(x)的最小值f(x)min=f(2)=3-
a.
令g(a)=3f(x)+|f'(a)-1|
∴g(a)≥9-4a+|a3-2a2|=
.
又9-4a+|a3-2a2|=
≥1.
∴g(a)=3f(x)+|f'(a)-1|的最小值为1.
∵x1,x2是f(x)的两个极值点,所以x1,x2是f'(x)=0的两根.
∴x1+x2=2,x1•x2=
| 1 |
| a |
又∵1<
| x2 |
| x1 |
∴2<
| x1+x2 |
| x1 |
∴1<
| 1 |
| x1 |
从而
| 1 |
| 3 |
∴
| 1 |
| a |
当
| 1 |
| 3 |
| 1 |
| a |
| 5 |
| 9 |
故 a∈(1,
| 9 |
| 5 |
(Ⅱ)当x≥2时,f'(x)单调递增
∴f'(x)≥f'(2)=1.
∴f(x)单调递增
∴f(x)的最小值f(x)min=f(2)=3-
| 4 |
| 3 |
令g(a)=3f(x)+|f'(a)-1|
∴g(a)≥9-4a+|a3-2a2|=
|
又9-4a+|a3-2a2|=
|
∴g(a)=3f(x)+|f'(a)-1|的最小值为1.
点评:本题主要考查利用导数研究函数的单调性等性质,及导数应用等基础知识,同时考查抽象概括、推理论证能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
cos50°cos20°+sin50°sin20°的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若三点A(2,3),B(3,4),C(a,b)共线,则有( )
| A、a=3,b=-5 |
| B、a-b+1=0 |
| C、2a-b=3 |
| D、a-2b=0 |
已知f(x)=
,则f(-8)等于( )
|
| A、-1 | B、0 | C、1 | D、2 |
数列{an}中,a1=3,a2=6,an+2=an+1-an,那么a6=( )
| A、-2 | B、-3 | C、-6 | D、-8 |
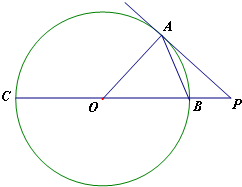 如图,点A在直径为15的⊙O上,PBC是过点O的割线,且PA=10,PB=5.
如图,点A在直径为15的⊙O上,PBC是过点O的割线,且PA=10,PB=5.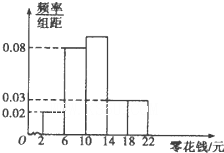 为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为
为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为