题目内容
已知平面上两点M(-1,0),N(1,0),若曲线上存在点P使得|PM|+|PN|=4,则称该曲线为“1?
曲线”,下列曲线中是“1?
曲线”的是 (将正确答案的序号写到横线上)
①x2+y2=4
②
+
=1
③
-
=1
④y2=8x.
| 1 |
| 2 |
| 1 |
| 2 |
①x2+y2=4
②
| x2 |
| 3 |
| y2 |
| 4 |
③
| x2 |
| 25 |
| y2 |
| 16 |
④y2=8x.
考点:椭圆的定义
专题:圆锥曲线的定义、性质与方程
分析:由题意,动点P的轨迹是椭圆,写出椭圆的方程以及x、y的取值范围;
由此判定①、②、③、④中方程所表示的几何图形以及x、y的取值范围,得出正确的序号.
由此判定①、②、③、④中方程所表示的几何图形以及x、y的取值范围,得出正确的序号.
解答:
解:根据题意,动点P的轨迹是椭圆,且焦点为M(-1,0),N(1,0),2a=4;
∴a=2,c=1,b=
;
∴椭圆的方程为
+
=1,x∈[-2,2],y∈[-
,
];
对于①,x2+y2=4表示圆心在原点,半径为2的圆,且x∈[-2,2],y∈[-2,2],∴该圆上存在满足条件的点P;∴①正确.
对于②,
+
=1表示椭圆,且x∈[-
,
],y∈[-2,2],∴该椭圆上存在满足条件的点P;∴②正确.
对于③,
-
=1表示双曲线,且x∈(-∞,-5]∪[5,+∞),y∈(-∞,-4]∪[4,+∞),∴该双曲线上不存在满足条件的点P;∴③错误.
对于④,y2=8x表示抛物线,且x∈[0,+∞),y∈R,∴该抛物线上存在满足条件的点P;∴④正确.
综上,正确的序号是①②④;
故答案为:①②④.
∴a=2,c=1,b=
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 3 |
对于①,x2+y2=4表示圆心在原点,半径为2的圆,且x∈[-2,2],y∈[-2,2],∴该圆上存在满足条件的点P;∴①正确.
对于②,
| x2 |
| 3 |
| y2 |
| 4 |
| 3 |
| 3 |
对于③,
| x2 |
| 25 |
| y2 |
| 16 |
对于④,y2=8x表示抛物线,且x∈[0,+∞),y∈R,∴该抛物线上存在满足条件的点P;∴④正确.
综上,正确的序号是①②④;
故答案为:①②④.
点评:本题考查了圆锥曲线的方程以及性质的应用问题,解题时应熟练地掌握几类常用的圆锥曲线方程与它们的几何性质,是中档题.

练习册系列答案
相关题目
已知f(x)=
,则f(-8)等于( )
|
| A、-1 | B、0 | C、1 | D、2 |
下列哪个函数的图象只需平移变换即可得到f(x)=sinx+cosx的函数图象( )
A、f1(x)=
| ||||||||
| B、f2(x)=sinx | ||||||||
C、f3(x)=
| ||||||||
D、f4(x)=
|
 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=10,ED=3,求BC的长.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=10,ED=3,求BC的长.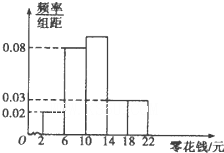 为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为
为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为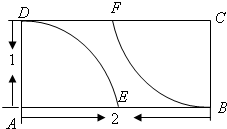 如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是