题目内容
3．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a=3，b=4，C=60°．（1）求c的值；
（2）求sinB的值．
分析 （1）由余弦定理求得c的值；
（2）由正弦定理求得sinB的值．
解答 解：（1）△ABC中，a=3，b=4，C=60°，
由余弦定理得，
c2=a2+b2-2abcosC=32+42-2×3×4×cos60°=13，
解得c=$\sqrt{13}$；
（2）由正弦定理，$\frac{b}{sinB}$=$\frac{c}{sinC}$，
∴sinB=$\frac{bsinC}{c}$=$\frac{4×sin60°}{\sqrt{13}}$=$\frac{2\sqrt{39}}{13}$．
点评 本题考查了正弦、余弦定理的应用问题，是基础题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
14．某考点2016年参加教师资格考试的人群由两部分组成，分别为在职人员与社会人员，现利用随机抽样的方法抽取50名参考人员研究它们的考试成绩，并将考试成绩和频数统计如下表所示：
将频率作为概率，解决下列问题：
（1）在这50名参考人员中任取一位，求分数不低于105分的概率；
（2）为了进一步了解这些参考人员的得分情况，再从分数在[65，75）的参考人员A，B，C中选出2位，从分数在[115，150）中的参考人员D，E，F，G，H中选出1位进行研究，求A和D同时被选到的概率．
| 组别 | [65，75） | [75，85） | [85，95） | [95，105） | [105，115） | [115，150） |
| 频数 | 3 | 4 | 13 | 15 | 10 | 5 |
（1）在这50名参考人员中任取一位，求分数不低于105分的概率；
（2）为了进一步了解这些参考人员的得分情况，再从分数在[65，75）的参考人员A，B，C中选出2位，从分数在[115，150）中的参考人员D，E，F，G，H中选出1位进行研究，求A和D同时被选到的概率．
18．某连锁经营公司所属5个零售店某月的销售额和利润额资料如表：
（Ⅰ）用最小二乘法计算利润额y对销售额x的回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（Ⅱ）当销售额为4（千万元）时，估计利润额的大小．
（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
| 商店名称 | A | B | C | D | E |
| 销售额x（千万元） | 3 | 5 | 6 | 7 | 9 |
| 利润额y（千万元） | 2 | 3 | 3 | 4 | 5 |
（Ⅱ）当销售额为4（千万元）时，估计利润额的大小．
（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
12．下列说法正确的是（ ）
| A． | 都与直线a相交的两条直线确定一个平面 | |
| B． | 两条直线确定一个平面 | |
| C． | 过一条直线的平面有无数多个 | |
| D． | 两个相交平面的交线是一条线段 |
13．
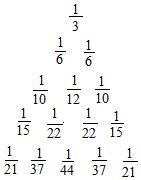如图所示的数阵中，用A（m，n）表示第m行的第n个数，则依次规律A（8，2）为（ ）
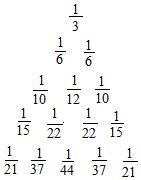如图所示的数阵中，用A（m，n）表示第m行的第n个数，则依次规律A（8，2）为（ ）| A． | $\frac{1}{45}$ | B． | $\frac{1}{86}$ | C． | $\frac{1}{122}$ | D． | $\frac{1}{167}$ |