题目内容
18.某连锁经营公司所属5个零售店某月的销售额和利润额资料如表:| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
(Ⅱ)当销售额为4(千万元)时,估计利润额的大小.
(注:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
分析 (Ⅰ)设出方程,利用已知条件,转化求解回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$即可;
(Ⅱ)利用回归直线方程,代入求解即可.
解答 (本小题满分8分)
解 (Ⅰ)设回归直线的方程是:$\widehaty=bx+a$,$\overline y=3.4,\overline x=6$,
∴$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{-3×({-1.4})+({-1})×({-0.4})+1×0.6+3×1.6}}{9+1+1+9}=\frac{10}{20}=\frac{1}{2}$a=0.4,
∴y对销售额x的回归直线方程为:$\widehaty=0.5x+0.4$;------(6分)
(Ⅱ)当销售额为4(千万元)时,利润额为:$\hat y=0.5×4+0.4=2.4$(千万元).---(8分)
点评 本题考查回归直线方程的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
6.小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为( )
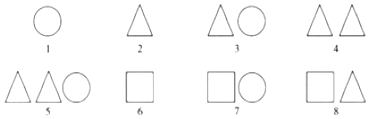

| A. | 670 | B. | 672 | C. | 335 | D. | 336 |
8.已知等边三角形的边长为1,那么它的平面直观图面积为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{8}$ | C. | $\frac{\sqrt{6}}{8}$ | D. | $\frac{\sqrt{6}}{16}$ |