题目内容
13.已知函数f(x)=x-e${\;}^{\frac{x}{a}}$(a>0)有两个相异零点x1、x2,且x1<x2,求证:$\frac{{x}_{1}}{{x}_{2}}$<$\frac{e}{a}$.分析 求出原函数的导函数,得到函数的单调区间,再由已知可得a>e,进一步得到x1<a<alna<x2,然后利用放缩法证得$\frac{{x}_{1}}{{x}_{2}}$<$\frac{e}{a}$.
解答 证明:f′(x)=1-$\frac{1}{a}{e}^{\frac{x}{a}}$,
由f′(x)>0,得x<alna,由f′(x)<0,得x>alna,
∴f(x)在(-∞,alna)上单调递增,在(alna,+∞)上单调递减,
∴f(x)在x=alna处取得极大值,且为最大值等于f(alna)=alna-a.
由函数f(x)=x-e${\;}^{\frac{x}{a}}$(a>0)有两个相异零点x1、x2,可得alna-a>0,
即a>e.
∵f(a)=a-e>0,
∴x1<a<alna<x2,
∴${x}_{2}-{x}_{1}>alna-a=-aln\frac{e}{a}$,
即${x}_{1}-{x}_{2}<aln\frac{e}{a}$,
则$\frac{1}{a}({x}_{1}-{x}_{2})$$<ln\frac{e}{a}$,
∵${x}_{1}={e}^{\frac{{x}_{1}}{a}}$,${x}_{2}={e}^{\frac{{x}_{2}}{a}}$,
∴$\frac{{x}_{1}}{{x}_{2}}=\frac{{e}^{\frac{{x}_{1}}{a}}}{{e}^{\frac{{x}^{2}}{a}}}={e}^{\frac{1}{a}({x}_{1}-{x}_{2})}$$<{e}^{ln\frac{e}{a}}=\frac{e}{a}$.
点评 本题考查导数在最大值与最小值中的应用,考查利用导数证明函数不等式,考查逻辑思维能力与推理运算能力,是中档题.

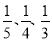 .求:
.求: