题目内容
15.在△ABC中,|$\overrightarrow{BC}$|=4,△ABC的内切圆切BC于D点,且|$\overrightarrow{BD}$|-|$\overrightarrow{CD}$|=2$\sqrt{2}$,则顶点A的轨迹方程为$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1(x>$\sqrt{2}$).分析 由题意画出图形,由图可知∴|AB|-|AC|=|BE|-|CF|=|$\overrightarrow{BD}$|-|$\overrightarrow{CD}$|=2$\sqrt{2}$,即点A的轨迹为以B,C为焦点的双曲线的右支(y≠0),顶点A的轨迹方程可求.
解答 解:如图,
设E、F分别为圆与AB、AC的两个切点,
则|BE|=|BD|,|CD|=|CF|,
又|AE|=|AF|,
∴|AB|-|AC|=|BE|-|CF|=|$\overrightarrow{BD}$|-|$\overrightarrow{CD}$|=2$\sqrt{2}$,
∴点A的轨迹为以B,C为焦点的双曲线的右支(y≠0),
且a=$\sqrt{2}$,c=2,
∴b=$\sqrt{{2}^{2}{-(\sqrt{2})}^{2}}$=$\sqrt{2}$,
∴轨迹方程为$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1(x>$\sqrt{2}$).
故答案为:$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1(x>$\sqrt{2}$).
点评 本题考查了双曲线的定义与平面几何知识在求解圆锥曲线问题中的应用问题,是综合题.

练习册系列答案
相关题目
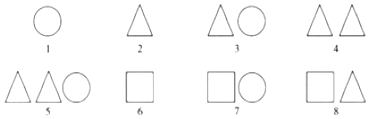
6.小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为( )

| A. | 670 | B. | 672 | C. | 335 | D. | 336 |
20.如图是某算法的程序框图,若程序运行后输出的结果是14,则判断框内填入的条件可以是( )


| A. | S≥10? | B. | S≥14? | C. | n>4? | D. | n>5? |