题目内容
判断并证明f(x)=
在区间(-1,+∞)上的单调性,并求出f(x)在[0,5]的最值.
| 3 |
| x+1 |
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:本题先利用函数的单调性定义证明函数的单调性,再利用函数的单调性求出函数在区间上的最值,得到本题结论.
解答:
解:f(x)在区间(-1,+∞)上单调递减,证明如下:
令-1<x1<x2,则
f(x1)-f(x2)=
-
=
.
∵-1<x1<x2,
∴x1+1>0,x2+1>0,x2-x1>0,
∴
>0⇒f(x1)-f(x2)>0.
即 f(x1)>f(x2),
∴f(x)=
在区间(-1,+∞)上单调递减.
易知f(x)在[0,5]上单调递减,
∵0≤x≤5,
∴f(5)≤f(x)≤f(0).
当x=0时,f(x)有最大值f(0)=3,
当x=5时,f(x)有最小值f(5)=
.
令-1<x1<x2,则
f(x1)-f(x2)=
| 3 |
| x1+1 |
| 3 |
| x2+1 |
=
| 3(x2-x1) |
| (x1+1)(x2+1) |
∵-1<x1<x2,
∴x1+1>0,x2+1>0,x2-x1>0,
∴
| 3(x2-x1) |
| (x1+1)(x2+1) |
即 f(x1)>f(x2),
∴f(x)=
| 3 |
| x+1 |
易知f(x)在[0,5]上单调递减,
∵0≤x≤5,
∴f(5)≤f(x)≤f(0).
当x=0时,f(x)有最大值f(0)=3,
当x=5时,f(x)有最小值f(5)=
| 1 |
| 2 |
点评:本题考查了函数的单调性和最值,本题难度不大,属于基础题.

练习册系列答案
相关题目
若函数f(x)=x2+4x+6,则f(x)在[-3,0)上的值域为( )
| A、[2,6] |
| B、[2,6) |
| C、[2,3] |
| D、[3,6] |
在圆的方程x2+y2+Dx+Ey+F=0中,若D2=E2>4F,则( )
| A、圆与两坐标轴都相切 |
| B、圆与两坐标轴都相交 |
| C、圆与两坐标轴都相离 |
| D、圆心到两坐标轴的距离相等 |
已知a,b,c∈R,下列说法正确的是( )
| A、a>b⇒ac2>bc2 | ||||
B、
| ||||
C、a>b>0⇒
| ||||
| D、a>b⇒a2>b2 |
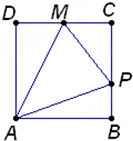 如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )
如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )A、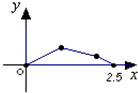 |
B、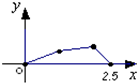 |
C、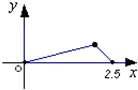 |
D、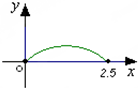 |
下列函数中,既是奇函数又在定义域内单调递减的函数为( )
A、y=
| ||
| B、y=lgx | ||
| C、y=sinx | ||
D、y=
|