题目内容
已知函数f(x)=xm2-2m-3(m∈N*)的图象关于y轴对称,且f(3)>f(5),求满足(a+1)-
<(3-2a)-
的a的取值范围.
| m |
| 3 |
| m |
| 3 |
考点:幂函数的性质
专题:函数的性质及应用
分析:根据幂函数在(0,+∞)上是减函数,可以确定m-3<0,再根据的图象关于y轴对称,即可得到f(x)为偶函数,从而确定m的值,构造函数g(x)=,利用幂函数的性质,即可列出关于a的不等式,求解不等式可以求得a的取值范围.
根据幂函数在(0,+∞)上函数值随x增大而减小,得到3m-9<0,然后根据函数图象关于y轴对称,得到函数为偶函数,确定m的值,然后解不等式即可.
根据幂函数在(0,+∞)上函数值随x增大而减小,得到3m-9<0,然后根据函数图象关于y轴对称,得到函数为偶函数,确定m的值,然后解不等式即可.
解答:
解:解:∵函数f(x)=xm2-2m-3(m∈N*)在(0,+∞)上递减,
∴m2-2m-3<0,解得-1<m<3,
∵m∈N+,
∴m=1,2,
又∵函数的图象关于y轴对称,
∴f(x)为偶函数,
∴m2-2m-3是偶数,
又m=1时,m2-2m-3=-4为偶数;
m=2时,m2-2m-3=3为奇数,
∴m=1,
令g(x)=x -
,
∴g(x)=x -
在(-∞,0)和(0,+∞)上均为减函数,
∵(a+1)-
<(3-2a)-
,
∴a+1>3-2a>0,或0>a+1>3-2a,或a+1<0<3-2a,
解得a<-1,或
<a<
,
故a的取值范围为{a|a<-1或
<a<
,}.
∴m2-2m-3<0,解得-1<m<3,
∵m∈N+,
∴m=1,2,
又∵函数的图象关于y轴对称,
∴f(x)为偶函数,
∴m2-2m-3是偶数,
又m=1时,m2-2m-3=-4为偶数;
m=2时,m2-2m-3=3为奇数,
∴m=1,
令g(x)=x -
| 1 |
| 3 |
∴g(x)=x -
| 1 |
| 3 |
∵(a+1)-
| m |
| 3 |
| m |
| 3 |
∴a+1>3-2a>0,或0>a+1>3-2a,或a+1<0<3-2a,
解得a<-1,或
| 2 |
| 3 |
| 3 |
| 2 |
故a的取值范围为{a|a<-1或
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题主要考查幂函数的图象和性质,利用条件求出m是解决本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
在△ABC中,M是BC的中点,AM=3,BC=10,则
•
=( )
| AB |
| AC |
| A、9 | B、16 |
| C、-16 | D、与三角形形状有关 |
 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
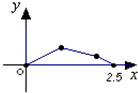
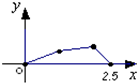
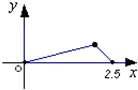
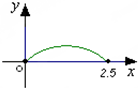
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若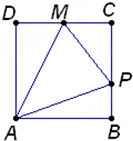 如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )
如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )