题目内容
已知△ABC的顶点A(0,1),BC边所在的直线方程为x-4y-2=0,AC边所在直线的方程为x=0,AB边的中点坐标为E(1,
).
(1)求△ABC的顶点B、C的坐标;
(2)过点F(-1,-2)的直线分别交x轴、y轴的负半轴于M,N两点,当|FM|•|FN|最小时,求直线l的方程.
| 1 |
| 2 |
(1)求△ABC的顶点B、C的坐标;
(2)过点F(-1,-2)的直线分别交x轴、y轴的负半轴于M,N两点,当|FM|•|FN|最小时,求直线l的方程.
考点:直线的一般式方程
专题:直线与圆
分析:(1)联立
,解得C点的坐标.利用中点坐标公式可得B点的坐标.
(2)设直线l的方程为y+2=k(x+1),分别令x=0,y=0,可得M,N的坐标.再利用两点之间的距离公式、基本不等式的性质即可得出.
|
(2)设直线l的方程为y+2=k(x+1),分别令x=0,y=0,可得M,N的坐标.再利用两点之间的距离公式、基本不等式的性质即可得出.
解答:
解:(1)∵BC边所在的直线方程为x-4y-2=0,AC边所在直线的方程为x=0,
联立
,解得x=0,y=-
.
∴C(0,-
),
又∵AB边的中点坐标为E(1,
).
∴
,解得xB=2,yB=0.
∴B(2,0).
(2)设直线l的方程为y+2=k(x+1),
令x=0,得y=k-2,则M(
-1,0)
令y=0,得x=
-1,则N(0,k-2).
∴|FM|•|FN|=
•
=
≥4,
当且仅当k2=
,即k=±1时等号成立,
但k<0,故直线l的方程为:x+y+3=0.
联立
|
| 1 |
| 2 |
∴C(0,-
| 1 |
| 2 |
又∵AB边的中点坐标为E(1,
| 1 |
| 2 |
∴
|
∴B(2,0).
(2)设直线l的方程为y+2=k(x+1),
令x=0,得y=k-2,则M(
| 2 |
| k |
令y=0,得x=
| 2 |
| k |
∴|FM|•|FN|=
|
| k2+1 |
4k2+
|
当且仅当k2=
| 1 |
| k2 |
但k<0,故直线l的方程为:x+y+3=0.
点评:本题考查了直线的方程、中点坐标公式、两点之间的距离公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
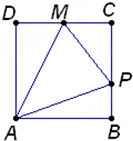 如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )
如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )A、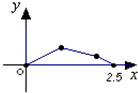 |
B、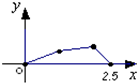 |
C、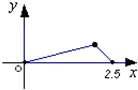 |
D、 |
下列函数中,既是奇函数又在定义域内单调递减的函数为( )
A、y=
| ||
| B、y=lgx | ||
| C、y=sinx | ||
D、y=
|
等差数列{an}的公差为2,a2+a8=16,则a6=( )
| A、6 | B、8 | C、10 | D、12 |
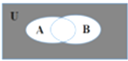 已知U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},则Venn图中阴影部分所表示的集合为( )
已知U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},则Venn图中阴影部分所表示的集合为( )| A、{3} |
| B、{4,5,6,7,8} |
| C、{7,8} |
| D、{1,2,7,8} |
 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若