题目内容
已知x、y取值如表:画散点图分析可知:y与x线性相关,且求得回归方程为
=bx+a中a=50,猜想x=4时,y的值为( )
| ? |
| y |
| x | 14 | 12 | 8 | 6 |
| y | 22 | 25 | 35 | 38 |
| A、40 | B、42 | C、44 | D、46 |
考点:线性回归方程
专题:概率与统计
分析:利用回归直线方程经过样本中心求出b,代入x=4即可求出结果.
解答:
解:因为回归直线方程经过样本中心,
所以
=
=10.
=
=30.
=bx+a中a=50,可得30=10b+50,b=-2,
∴回归直线方程为:
=-2x+50,
x=4时,y=42.
故选:B.
所以
. |
| x |
| 14+12+8+6 |
| 4 |
. |
| y |
| 22+25+35+38 |
| 4 |
| ? |
| y |
∴回归直线方程为:
| ? |
| y |
x=4时,y=42.
故选:B.
点评:本题考查回归直线方程的应用,回归直线方程经过样本中心是解题的关键.

练习册系列答案
相关题目
在△ABC中,M是BC的中点,AM=3,BC=10,则
•
=( )
| AB |
| AC |
| A、9 | B、16 |
| C、-16 | D、与三角形形状有关 |
在圆的方程x2+y2+Dx+Ey+F=0中,若D2=E2>4F,则( )
| A、圆与两坐标轴都相切 |
| B、圆与两坐标轴都相交 |
| C、圆与两坐标轴都相离 |
| D、圆心到两坐标轴的距离相等 |
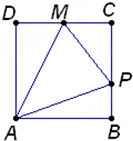 如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )
如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )A、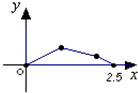 |
B、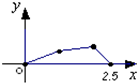 |
C、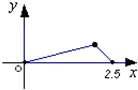 |
D、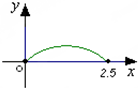 |
下列函数中,既是奇函数又在定义域内单调递减的函数为( )
A、y=
| ||
| B、y=lgx | ||
| C、y=sinx | ||
D、y=
|
已知全集U=R,集合A={x|x2<4},B={x|
≤0},A∩(∁UB)=( )
| 1-x |
| x |
| A、(0,1) |
| B、[0,1) |
| C、(-2,0)∪[1,2) |
| D、[-2,2) |