题目内容
14.已知函数$f(x)=\sqrt{3}sinxcosx-{cos^2}x+\frac{1}{2}\;(x∈R)$.(1)求函数f(x)的单调递增区间;
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移$\frac{π}{6}$个单位长度,得g(x)的图象,求函数y=g(x)在x∈[0,π]上的最大值及最小值.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(2x-$\frac{π}{6}$),由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$,即可解得函数f(x)的单调递增区间.
(2)利用函数y=Asin(ωx+φ)的图象变换可得g(x)=sin(x-$\frac{π}{3}$),由x∈[0,π]得:$x-\frac{π}{3}∈[{-\frac{π}{3},\frac{2π}{3}}]$,利用正弦函数的图象即可解得函数y=g(x)在x∈[0,π]上的最大值及最小值.
解答 (本题满分为12分)
解:(1)∵$f(x)=\sqrt{3}sinxcosx-{cos^2}x+\frac{1}{2}=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}{cos^2}x=sin(2x-\frac{π}{6})$,
∴由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$,得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}\;(k∈Z)$,
∴函数f(x)的单调递增区间为:$[{kπ-\frac{π}{6},kπ+\frac{π}{3}}]\;(k∈Z)$.…(6分)
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移$\frac{π}{6}$个单位,得$g(x)=sin(x-\frac{π}{3})$,
∵x∈[0,π]得:$x-\frac{π}{3}∈[{-\frac{π}{3},\frac{2π}{3}}]$,
∴$sin(x-\frac{π}{3})∈[{-\frac{{\sqrt{3}}}{2},1}]$.
∴当x=0时,$g(x)=sin(x-\frac{π}{3})$有最小值$-\frac{{\sqrt{3}}}{2}$,
当$x=\frac{5π}{6}$时,$g(x)=sin(x-\frac{π}{3})$有最大值1.…(12分)
点评 本题主要考查了三角函数恒等变换的应用,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,属于中档题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | $\frac{π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
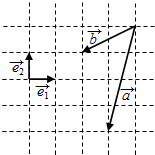 向量$\overrightarrow{e_1},\;\overrightarrow{e_2},\;\overrightarrow a,\;\overrightarrow b$在正方形网格中的位置如图所示,若$\overrightarrow a-\overrightarrow b=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则x=1,y=-3.
向量$\overrightarrow{e_1},\;\overrightarrow{e_2},\;\overrightarrow a,\;\overrightarrow b$在正方形网格中的位置如图所示,若$\overrightarrow a-\overrightarrow b=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则x=1,y=-3.