题目内容
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{5}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
分析 根据向量的夹角公式,以及向量的垂直,向量模计算即可
解答 解:设$\overrightarrow{a}$与$\vec b$的夹角为θ,
∵|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{5}$,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}$•$\overrightarrow{b}$=4,
|$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$=20,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-4,|$\overrightarrow{b}$|=2$\sqrt{2}$
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-4}{2×2\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$,
∵0≤θ≤π,
∴θ=$\frac{3π}{4}$,
故选:C.
点评 本题考查了向量的数量积的运算以及向量的模的计算,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | (0,1,1) | B. | (0,1,-3) | C. | (-1,0,3) | D. | (-1,0,-5) |
| A. | x>1 | B. | 若a>b,则a2>ab | ||
| C. | y=sinx是奇函数吗? | D. | 若a-2是无理数,则a是无理数 |
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
| A. | {2} | B. | {2,3} | C. | {1,2,3} | D. | {1,2,3,4} |
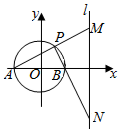 已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.
已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.