题目内容
19．
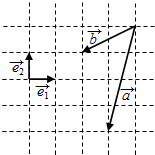向量$\overrightarrow{e_1}，\;\overrightarrow{e_2}，\;\overrightarrow a，\;\overrightarrow b$在正方形网格中的位置如图所示，若$\overrightarrow a-\overrightarrow b=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，则x=1，y=-3．
分析 结合图形，根据向量加法和数乘的几何意义便可用$\overrightarrow{{e}_{1}}，\overrightarrow{{e}_{2}}$表示出$\overrightarrow{a}，\overrightarrow{b}$，然后进行向量的数乘运算即可得出$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{{e}_{1}}-3\overrightarrow{{e}_{2}}$，这样根据平面向量基本定理即可求出x，y的值．
解答 解：根据图形得：$\overrightarrow{a}=-\overrightarrow{{e}_{1}}-4\overrightarrow{{e}_{2}}，\overrightarrow{b}=-2\overrightarrow{{e}_{1}}-\overrightarrow{{e}_{2}}$；
∴$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{{e}_{1}}-3\overrightarrow{{e}_{2}}$；
又$\overrightarrow{a}-\overrightarrow{b}=x\overrightarrow{{e}_{1}}+y\overrightarrow{{e}_{2}}$；
∴x=1，y=-3．
故答案为：1，-3．
点评 考查向量加法和数乘的几何意义，以及向量的数乘运算，平面向量基本定理．
练习册系列答案
相关题目
10．下列语句是真命题的是（ ）
| A． | x＞1 | B． | 若a＞b，则a2＞ab | ||
| C． | y=sinx是奇函数吗？ | D． | 若a-2是无理数，则a是无理数 |
4．已知命题p：?x∈R，x2-x-2≥0，那么命题?p为（ ）
| A． | ?x∈R，x2-x-2≤0 | B． | ?x∈R，x2-x-2＜0 | C． | ?x∈R，x2-x-2≤0 | D． | ?x∈R，x2-x-2＜0 |
11．已知集合A={1，2}，B={2，3，4}，那么集合A∩B等于（ ）
| A． | {2} | B． | {2，3} | C． | {1，2，3} | D． | {1，2，3，4} |
8．
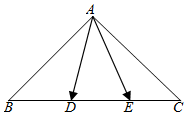如图，在等腰直角三角形ABC中，AB=AC=$\sqrt{2}$，D，E是线段BC上的点，且DE=$\frac{1}{3}$BC，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是（ ）
如图，在等腰直角三角形ABC中，AB=AC=$\sqrt{2}$，D，E是线段BC上的点，且DE=$\frac{1}{3}$BC，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是（ ）| A． | $[{\frac{8}{9}，\;\frac{4}{3}}]$ | B． | $[{\frac{4}{3}，\;\frac{8}{3}}]$ | C． | $[{\frac{8}{9}，\;\frac{8}{3}}]$ | D． | $[{\frac{4}{3}，\;+∞}）$ |
9．已知函数f（x）=x-alnx在区间（0，2]上单调递减，则实数a的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （0，2） | C． | （$\frac{1}{2}$，+∞） | D． | [2，+∞） |