题目内容
6．某几何体的三视图如图所示，则该几何体的体积等于56．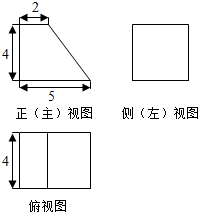
分析 根据三视图知几何体为一平放的直四棱柱，结合图中数据求出四棱柱的体积．
解答 解：由三视图知几何体为一平放的直四棱柱，
且四棱柱的底面为直角梯形，高为4；
又直角梯形的上底为2，下底为5，高为4，
所以直角梯形的面积为$\frac{1}{2}$×（2+5）×4=14，
所以该四棱柱的体积为V=14×4=56．
故答案为：56．
点评 本题考查了由三视图求几何体体积的应用问题，解题的关键是判断几何体的形状，是基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
17．已知cosα=$\frac{1}{3}$，则sin（$\frac{π}{2}$+α）=（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | -$\frac{2\sqrt{2}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
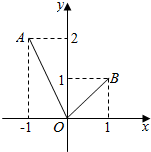如图，定义在[-1，1]上的函数f（x）的图象为折线AOB．若方程f（x）-mx-m=0有两个不等的实根，则实数m的取值范围是（0，$\frac{1}{2}$]．
11．已知集合A={1，2}，B={2，3，4}，那么集合A∩B等于（ ）
| A． | {2} | B． | {2，3} | C． | {1，2，3} | D． | {1，2，3，4} |