题目内容

4．已知函数f（x）为奇函数，且当x＞0时，$f（x）={x^2}+\frac{2}{x}$，则f（-1）=（　　）
A．-2B．2C．-3D．3

分析 由条件利用函数的奇偶性和单调性的性质可得 f（-1）=-f（1），运算求得结果．

解答 解：∵已知函数f（x）为奇函数，且当x＞0时，$f（x）={x^2}+\frac{2}{x}$，
∴f（-1）=-f（1）=-（1+2）=-3，
故选：C．

点评 本题主要考查函数的奇偶性的应用，属于基础题．

练习册系列答案
相关题目
4．已知关于x的一元二次方程x2+2ix+（a+1）=0有实数解，则实数a的取值范围是{-1}．
5．在△ABC中，若a=（$\sqrt{3}$-1）b，C=30°，则A=$\frac{π}{4}$．
12．已知A（1，2，-1），B（5，6，7），则直线AB与平面xoz交点的坐标是（　　）
A．（0，1，1）B．（0，1，-3）C．（-1，0，3）D．（-1，0，-5）
19．“b≠0”是“复数a+bi（a，b∈R）是纯虚数”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
9．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$离心率为$\frac{{\sqrt{2}}}{2}$，点P（0，1）在短轴CD上，且$\overrightarrow{PC}•\overrightarrow{PD}=-1$．
（I）求椭圆E的方程；
（Ⅱ）过点P的直线l与椭圆E交于A，B两点．
（i）若$\overrightarrow{PB}=\frac{1}{2}\overrightarrow{AP}$，求直线l的方程；
（ii）在y轴上是否存在与点P不同的定点Q，使得$\frac{{\left|{QA}\right|}}{{\left|{QB}\right|}}=\frac{{\left|{PA}\right|}}{{\left|{PB}\right|}}$恒成立，若存在，求出点Q的坐标，若不存在，请说明理由．
16．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点$P（2，\sqrt{3}）$，且它的离心率为$\frac{1}{2}$．
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）与圆（x-1）2+y2=1相切的直线l：y=kx+t（k∈R，t∈R）交椭圆E于M、N两点，若椭圆E上一点C满足$\overrightarrow{OM}+\overrightarrow{ON}=λ\overrightarrow{OC}$（O为坐标原点），求实数λ的取值范围．
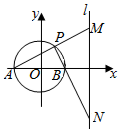13．已知圆O的直径AB=4，定直线l到圆心的距离为6，且直线l⊥直线AB．点P是圆上异于A、B的任意一点，直线PA、PB分别交l于M、N点．如图，以AB为x轴，圆心O为原点建立平面直角坐标系xOy．
（1）若∠PAB=30°，求以MN为直径的圆的方程；
（2）当点P变化时，求证：以MN为直径的圆必过圆O内的一定点．
14．已知函数$f（x）=\sqrt{3}sinxcosx-{cos^2}x+\frac{1}{2}\;（x∈R）$．
（1）求函数f（x）的单调递增区间；
（2）函数f（x）的图象上所有点的横坐标扩大到原来的2倍，再向右平移$\frac{π}{6}$个单位长度，得g（x）的图象，求函数y=g（x）在x∈[0，π]上的最大值及最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网