题目内容
5.y=$\sqrt{3}$cos(x+$\frac{π}{6}$)的最大值为$\sqrt{3}$.分析 由条件利用余弦函数的最大值,求得函数y的最大值.
解答 解:∵cos(x+$\frac{π}{6}$)的最大值为1,∴y=$\sqrt{3}$cos(x+$\frac{π}{6}$)的最大值为$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查余弦函数的最大值,属于基础题.

练习册系列答案
相关题目
10.下列语句是真命题的是( )
| A. | x>1 | B. | 若a>b,则a2>ab | ||
| C. | y=sinx是奇函数吗? | D. | 若a-2是无理数,则a是无理数 |
17.已知cosα=$\frac{1}{3}$,则sin($\frac{π}{2}$+α)=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
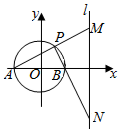 已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.
已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.