题目内容
设f(x)=ax3+bx2+cx+d(a≠0).已知五个方程的相异实根个数如下表所述﹕
α为关于f(x)的极大值﹐下列选项中正确的是( )
| f(x)-20=0 | 1 | f(x)+10=0 | 1 |
| f(x)-10=0 | 3 | f(x)+20=0 | 1 |
| f(x)=0 | 3 |
| A、0<α<10 |
| B、10<α<20 |
| C、-10<α<0 |
| D、-20<α<-10 |
考点:函数与方程的综合运用,函数的图象
专题:函数的性质及应用
分析:方程f(x)-k=0的相异实根数可化为方程f(x)=k的相异实根数,方程f(x)=k的相异实根数可化为函数y=f(x)与水平线y=k两图形的交点数﹒则依据表格可画出其图象的大致形状,从而判断极小值的取值范围.
解答:
解﹕方程f(x)-k=0的相异实根数可化为方程f(x)=k的相异实根数,
方程f(x)=k的相异实根数可化为函数y=f(x)与水平线y=k两图形的交点数﹒
依题意可得两图形的略图有以下两种情形﹕
(1)当a为正时,
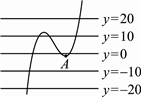
(2)当a为负时,

因极大值点a位于水平线y=10与y=20之间﹐
所以其y坐标α(即极大值)的范围为10<α<20﹒
故选:B﹒
方程f(x)=k的相异实根数可化为函数y=f(x)与水平线y=k两图形的交点数﹒
依题意可得两图形的略图有以下两种情形﹕
(1)当a为正时,

(2)当a为负时,

因极大值点a位于水平线y=10与y=20之间﹐
所以其y坐标α(即极大值)的范围为10<α<20﹒
故选:B﹒
点评:评:本题考查了方程的根与函数的图象的应用及数形结合思想的应用,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在极坐标方程中,曲线C的方程是ρ=4sinθ,过点(4,
)作曲线C的切线,切线长为( )
| π |
| 6 |
| A、4 | ||
| B、7 | ||
C、2
| ||
| D、3 2 |
在同一层有一排8间学术研讨室,现要安排4个不同学科的研讨会在这8间研讨室,要求任两个研讨会不相邻的安排方法数为( )
| A、5 | B、70 | C、120 | D、24 |
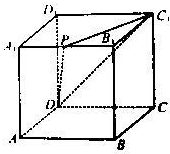 如图所示,若点P为正方体AC1的棱A1B1的中点,求截面PC1D和AA1B1B所成的锐二面角的余弦值.
如图所示,若点P为正方体AC1的棱A1B1的中点,求截面PC1D和AA1B1B所成的锐二面角的余弦值.