题目内容
5.(1)若x∈[0,2π].求函数y=$\sqrt{\frac{\sqrt{3}}{2}-sinx}$的定义域;(2)求函数y=$\sqrt{2-|x-4|}$+lg(-sinx)的定义域.
分析 根据三角函数,幂函数,对数函数即可求出函数的定义域.
解答 解:(1)$\frac{\sqrt{3}}{2}$-sinx≥0,即sinx≤$\frac{\sqrt{3}}{2}$,
∵x∈[0,2π],
∴0≤x≤$\frac{π}{3}$,或$\frac{2}{3}$π≤x≤2π,
∴函数y=$\sqrt{\frac{\sqrt{3}}{2}-sinx}$的定义域为[0,$\frac{π}{3}$]∪[$\frac{2}{3}$π,2π];
(2)要使函数y=$\sqrt{2-|x-4|}$+lg(-sinx)有意义,则2-|x-4|≥0,且-sinx>0,
即2≤x≤6,且-π+2kπ<x<2kπ,k∈Z,当k=1时,即为π<x≤6,
故函数y=$\sqrt{2-|x-4|}$+lg(-sinx)的定义域(π,6].
点评 本题考查了函数的定义域的求法,关键是掌握三角函数,对数函数,幂函数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知a>0且 a≠1,函数f(x)=$\frac{3{a}^{x}+1}{{a}^{x}+1}$+3loga$\frac{1+x}{1-x}$(-$\frac{1}{2}$≤x≤$\frac{1}{2}$),设函数f(x)的最大值是A,最小值是B,则( )
| A. | A-B=4 | B. | A+B=4 | C. | A-B=6 | D. | A+B=6 |
13.已知集合A={2,3,4},B={2,4,6},则A∩B=( )
| A. | {2} | B. | {2,4} | C. | {2,4,6} | D. | {2,3,4,6} |
10.已知在△ABC中,重心为P,$\overrightarrow{AB}$•$\overrightarrow{AC}$=-16,BC=10,则|$\overrightarrow{AP}$|等于( )
| A. | 5 | B. | 6 | C. | 4 | D. | 2 |
15.若执行如图所示的程序框图后,输出的结果是-29,则判断框中的整数k的值是( )
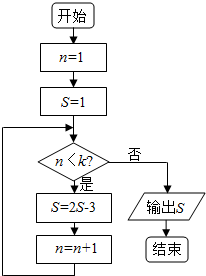

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |