题目内容
设函数f(x)＝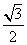
－
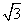sin2ωx－sinωxcosωx(ω>0)，且y＝f(x)图像的一个对称中心到最近的对称轴的距离为
.
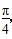(1)求ω的值；
(2)求f(x)在区间[π，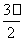
]上的最大值和最小值．
(1)f(x)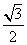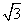＝－sin2ωx－sinωxcosωx
＝－·
－
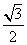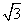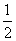sin2ωx
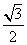＝cos2ωx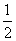－sin2ωx
＝－sin(2ωx－
)．
因为图像的一个对称中心到最近的对称轴的距离为，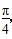
又ω>0，所以
，
因此ω＝1.
因此－1≤f(x)≤.
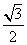故f(x)在区间[π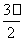，]上的最大值和最小值分别为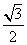，－1.
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
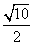，则tan2α＝( )
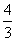B.
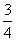
cos(x－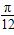
)，x∈R.
)的值；
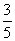，θ∈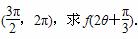
．
＝a1a4－a2a3.将函数f(x)＝
的图像向左平移
个单位，以下是所得函数图像的一个对称中心的是( )
，0) B．(
，0)
，0) D．(
，0)
＝
，则B的值为( )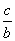
<cosA，则△ABC为________．
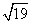km B．(
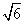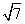－1)km
km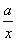
(x>0，a>0)在x＝3时取得最小值，则a＝________.