题目内容
已知等差数列{an}中,a3a7=-16,a4+a6=0.
(1)求an;
(2)若等差数列{an}为递增数列,设bn=(an+10)•2n,求数列{bn}的前n项和Sn.
(1)求an;
(2)若等差数列{an}为递增数列,设bn=(an+10)•2n,求数列{bn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由等差数列的性质可得:a3+a7=a4+a6=0,联立
,解得a3和a7,进而得到公差d.即可得到an.
(2)由等差数列{an}为递增数列,取d>0,可得an=2n-10.可得bn=n•2n+1.再利用“错位相减法”即可得出.
|
(2)由等差数列{an}为递增数列,取d>0,可得an=2n-10.可得bn=n•2n+1.再利用“错位相减法”即可得出.
解答:
解:(1)由等差数列的性质可得:a3+a7=a4+a6=0,
联立
,
解得a3=-a7=4,或a3=-a7=-4.
则公差d=-2或2.
∴an=a3+(n-3)d=10-2n或an=2n-10.
(2)∵等差数列{an}为递增数列,
∴an=2n-10.
∴bn=(an+10)•2n=n•2n+1.
∴Sn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,
可得2Sn=1×23+2×24+…+(n-1)×2n+1+n×2n+2,
∴-Sn=22+23+…+2n+1-n×2n+2=
-n×2n+2=(1-n)×2n-4,
∴Sn=(n-1)×2n+2+4.
联立
|
解得a3=-a7=4,或a3=-a7=-4.
则公差d=-2或2.
∴an=a3+(n-3)d=10-2n或an=2n-10.
(2)∵等差数列{an}为递增数列,
∴an=2n-10.
∴bn=(an+10)•2n=n•2n+1.
∴Sn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,
可得2Sn=1×23+2×24+…+(n-1)×2n+1+n×2n+2,
∴-Sn=22+23+…+2n+1-n×2n+2=
| 4×(2n-1) |
| 2-1 |
∴Sn=(n-1)×2n+2+4.
点评:本题考查了等差数列的通项公式及其性质、等比数列的前n项和公式、“错位相减法”等基础知识与基本技能方法,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
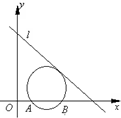 已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.
已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.