题目内容
设集合A={x|-2≤x≤5}，B={x|x2-3mx+2m2-m-1＜0}，若B=A∩B，求实数m的取值范围．
考点：交集及其运算
专题：计算题
分析：根据已知化简集合B，由B=A∩B，进一步分情况讨论、运算即可求出实数m的取值范围．
解答：
解：∵A={x|-2≤x≤5}，
B={x|x2-3mx+2m2-m-1＜0}={x|（x-2m-1）（x-m+1）=0}．
若B=A∩B，则A?B，
∴
，或
，
解得-1≤m≤2，或m不存在．
故m的取值范围：{m|-1≤m≤2}．
B={x|x2-3mx+2m2-m-1＜0}={x|（x-2m-1）（x-m+1）=0}．
若B=A∩B，则A?B，
∴
|
|
解得-1≤m≤2，或m不存在．
故m的取值范围：{m|-1≤m≤2}．
点评：本题考查了交集及其运算，属于基础题．
练习册系列答案
相关题目
已知（1-x）5=a0+a1x+a2x2+a3x3+a4x4+a5x5，那么（a0+a2+a4）（a1+a3+a5）的值等于（ ）
| A、-256 | B、256 |
| C、-512 | D、512 |
圆（x-2）2+（y+3）2=2的圆心和半径分别是（ ）
| A、（-2，3），1 | ||
| B、（2，-3），3 | ||
C、（-2，3），
| ||
D、（2，-3），
|
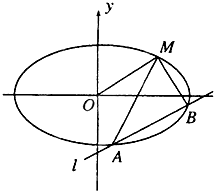如图，已知椭圆
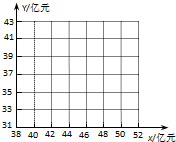某市居民1999～2003年货币收入x与购买商品支出Y的统计资料如下表所示：