Question

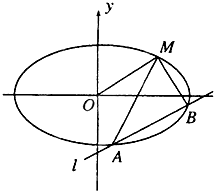如图，已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

3

2

，且经过点M（2，1）平行于OM的直线l在y轴上的截距为m（m≠0），l与椭圆有A、B两个不同的交点
（Ⅰ）求椭圆的方程；
（Ⅱ）求m的取值范围；
（Ⅲ）求证：直线MA、MB与x轴始终围成一个等腰三角形．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：圆锥曲线中的最值与范围问题

分析：（Ⅰ）设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，由已知得e=

c

a

=

3

2

，

4

a2

+

1

b2

=1，由此能求出椭圆方程．
（Ⅱ）l的方程为：y=

1

2

x+m，由

y= 1 2 x+m x2 8 + y2 2 =1

得x2+2mx+2m2-4=0，由此利用根的判别式能求出m的取值范围．
（III）设直线MA、MB的斜率分别为k₁，k₂，只需证明k₁+k₂=0即可证明直线MA、MB与x轴始终围成一个等腰三角形．

解答： （Ⅰ）解：设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)…（1分）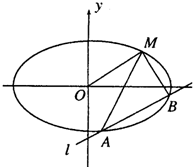
离心率e=

c

a

=

3

2

，
∴c2=

3

4

a2，解得b2=

1

4

a2，
由经过点M（2，1），

4

a2

+

1

b2

=1，
解得a²=8，b²=2，
∴椭圆方程为

x2

8

+

y2

2

=1．
（Ⅱ）解：∵直线l平行于OM，且在y轴上的截距为m
又KOM=

1

2

∴l的方程为：y=

1

2

x+m…（5分）
由

y= 1 2 x+m x2 8 + y2 2 =1

∴x2+2mx+2m2-4=0…（6分）
∵直线l与椭圆交于A、B两个不同点，

∴△=(2m)2-4(2m2-4)＞0， 解得-2＜m＜2，且m≠0…(8分)

（III）证明：设直线MA、MB的斜率分别为k₁，k₂，
只需证明k₁+k₂=0即可…（9分）
设A（x₁，y₁），B（x₂，y₂）则k1=

y1-1

x1-2

，k2=

y2-1

x2-2

由x2+2mx+2m2-4=0可得x1+x2+-2m，x1x2=2m2-4…（10分）
而k1+k2=

y1-1

x1-2

+

y2-1

x2-2

=

(y1-1)(x2-2)+(y2-1)(x1-2)

(x1-2)(x2-2)

= ( 1 2 x1+m-1)(x2-2)+( 1 2 x2+m-1)(x1-2) (x1-2)(x2-2) = x1x2+(m-2)(x1+x2)-4(m-1) (x1-2)(x2-2) = 2m2-4+(m-2)(-2m)-4(m-1) (x1-2)(x2-2)

= 2m2-4-2m2+4m-4m+4 (x1-2)(x2-2) =0…(13分) ∴k1+k2=0

故直线MA、MB与x轴始终围成一个等腰三角形．…（14分）

点评：本小题主要考查椭圆的标准方程，直线与椭圆的位置关系，考查转化与化归的思想方法，以及学生的运算能力．