题目内容
在△ABC中，a、b、c分别是角A，B，C 的对边．
（1）用向量知识证明：正弦定理：
=
=
=2R外（R为△ABC外接圆的半径）
（2）已知8b=5c，C=2B，求cosC的值．
（1）用向量知识证明：正弦定理：
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
（2）已知8b=5c，C=2B，求cosC的值．
考点：余弦定理,正弦定理
专题：计算题,证明题,解三角形
分析：（1）由
=
-
，两边平方，运用向量的数量积的定义和性质，注意结合同弧所对的圆心角是圆周角的2倍，运用二倍角的余弦公式，即可得到c=2RsinC，同理可证，a=2RsinA，b=2RsinB．
（2）直接利用正弦定理以及二倍角公式，求出sinB，cosB，然后利用平方关系式求出cosC的值即可．
| AB |
| OB |
| OA |
（2）直接利用正弦定理以及二倍角公式，求出sinB，cosB，然后利用平方关系式求出cosC的值即可．
解答：
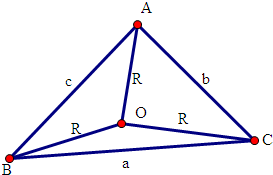（1）证明：∵
=
-
，
两边平方得，
2=（
-
）2，
即c2=R2+R2-2
•
=2R2-2R2•cos∠AOB=
2R2（1-cos2∠ACB）=4R2sin2∠ACB，
则c=2RsinC，
同理可证，a=2RsinA，b=2RsinB．
即有正弦定理：
=
=
=2R外（R为△ABC外接圆的半径）；
（2）∵在△ABC中，8b=5c，C=2B，
∴由正弦定理得：8sinB=5sinC=5sin2B=10sinBcosB，
∴cosB=
，
∵B为三角形内角，
∴B∈（0，
），C＜
，
∴sinB=
=
，
∴sinC=sin2B=2×
×
=
，
则cosC=
=
．
（1）证明：∵| AB |
| OB |
| OA |
两边平方得，
| AB |
| OB |
| OA |
即c2=R2+R2-2
| OA |
| OB |
2R2（1-cos2∠ACB）=4R2sin2∠ACB，
则c=2RsinC，
同理可证，a=2RsinA，b=2RsinB．
即有正弦定理：
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
（2）∵在△ABC中，8b=5c，C=2B，
∴由正弦定理得：8sinB=5sinC=5sin2B=10sinBcosB，
∴cosB=
| 4 |
| 5 |
∵B为三角形内角，
∴B∈（0，
| π |
| 4 |
| π |
| 2 |
∴sinB=
| 1-cos2B |
| 3 |
| 5 |
∴sinC=sin2B=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
则cosC=
| 1-sin2C |
| 7 |
| 25 |
点评：此题考查了正弦定理的向量证明及运用，同角三角函数间的基本关系，二倍角的正弦函数公式，熟练掌握正弦定理是解本题的关键．
练习册系列答案
习题精选系列答案
相关题目
若f（x）是偶函数，且当x∈[0，+∞）时，f（x）=x-1，则f（x）＜0的解集是（ ）
| A、（-1，0） |
| B、（-∞，1） |
| C、[0，1） |
| D、（-1，1） |
向如图所示的方砖上随机投掷一粒豆子，则该豆子落在阴影部分的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
