题目内容

已知P是△ABC所在的平面内一点，AB=4，
PA
+
PB
+
PC
=
0
，
PA
•
PB
=
PB
•
PC
=
PC
•
PA
，若点D、E分别满足
DC
=-
AC
，
BE
=3
EC
，则
AP
•
DE
=（　　）
A、8
B、
3
C、-4
3
D、-8
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由
PA
+
PB
+
PC
=
0
，推出P为重心，由于
PA
•
PB
=
PB
•
PC
=
PC
•
PA
，推出P又为垂心，故三角形ABC为等边三角形，边长为4，运用向量的合成与分解，将
AP
、
DE
用向量AB，AC表示，再化简
AP
•
DE
，运用等边三角形的特点，以及向量的模的公式和数量积的定义，即可得到答案．
解答： 解：∵
PA
+
PB
+
PC
=
0
，则
PA
+
PB
=-
PC
，
由平行四边形法则，得CP延长交AB于中点，
同理，BP延长交AC于中点，∴P为重心；
∵
PA
•
PB
=
PB
•
PC
=
PC
•
PA
，∴
PB
•（
PA
-
PC
）=0，
即PB⊥AC，同理PC⊥AB，∴P又为垂心，
故三角形ABC为等边三角形，边长为4，
又点D、E分别满足
DC
=-
AC
，
BE
=3
EC
，
则
AD
=2
AC
，
CE
=
1
4
CB
，
AP
=
2
3
×
1
2
（
AB
+
AC
）=
1
3
（
AB
+
AC
），
DE
=
AE
-
AD
=
AC
+
CE
-2
AC
=
1
4
CB
-
AC
=
AB
-5
AC
4
．
∴
AP
•
DE
=
1
12
（
AB
+
AC
）•（
AB
-5
AC
）
=
1
12
（
AB
2-5
AC
2-4
AB
•
AC
）
=
1
12
×（16-5×16-4×16×
1
2
）=-8．
故选D．
点评：本题考查两向量的数量积的运算，以及两向量的和、垂直的条件，考查三角形的重心和垂心，考查基本的运算能力，属于中档题．
练习册系列答案
相关题目
函数f（ax+b）=2m-f（-ax+c）的对称中心为
 
．
半径为R的球的内接正三棱柱的三个侧面积之和的最大值为（　　）
A、3
3
R2
B、
3
R2
C、2
2
R2
D、
2
R2
已知函数f（x）=
1
2x
-cosx，若
π
3
＜a＜b＜
5π
6
，则（　　）
A、f（a）＞f（b）
B、f（a）＜f（b）
C、f（a）=f（b）
D、f（a）f（b）＞0
若原点O和点F（-3，0）分别是双曲线
x2
a2
-y2=1（a＞0）的中心和左焦点，点P为双曲线右支上的任意一点，则
OP
•
FP
的取值范围为（　　）
A、[8+6
2
，+∞）
B、[-3，+∞）
C、[-
1
8
，+∞）
D、[
1
8
，+∞）
四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…这样交替进行下去，那么第2014次互换座位后，小兔坐在第（　　）号座位上．
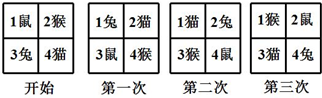
A、1B、2C、3D、4
已知向量
a
，
b
的夹角为
π
4
，且|
a
|=4，（
1
2
a
+
b
）•（2
a
-3
b
）=12，则向量
b
在向量
a
方向上的投影是（　　）
A、
2
B、4
C、4
2
D、1
已知正三角形ABC的边长是3，D是BC上的点，BD=1，则
AD
•
BC
=（　　）
A、-
9
2
B、-
3
2
C、
15
2
D、
5
2
已知函数f（x）=
4x+k•2x+1
4x+2x+1
．
（1）当k=2时，求函数f（x）的最大值；
（2）对定义域内的任意x都有|f（x）-1|≤k成立，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网