题目内容
已知向量
=(
,
sinx+
cosx)与
=(1,y)共线,设函数y=f(x).
(1)求函数f(x)最大值,并求出对应的x的集合;
(2)已知锐角△ABC 中的三个内角分别为 A、B、C,若有f(A-
)=
,边 BC=
,sinB=
,求△ABC 的面积.
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| b |
(1)求函数f(x)最大值,并求出对应的x的集合;
(2)已知锐角△ABC 中的三个内角分别为 A、B、C,若有f(A-
| π |
| 3 |
| 3 |
| 7 |
| ||
| 7 |
考点:三角函数中的恒等变换应用,正弦定理
专题:计算题
分析:(1)由向量
与
共线,既有
y-(
sinx+
cosx)=0,进而可求函数f(x)的表达式,从而求出函数f(x)的最大值,并求出对应的x的集合;
(2)由f(A-
)=
,可求出A的值,由正弦定理可求出AC,sinC的值,即可求出△ABC 的面积.
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(2)由f(A-
| π |
| 3 |
| 3 |
解答:
解:(1)因为向量
与
共线,所以
y-(
sinx+
cosx)=0,
则y=f(x)=2sin(x+
),所以f(x)的周期T=2π,
当x=2kπ+
,k∈Z,fmax=2.
(2)∵f(A-
)=
,
∴2sin(A-
+
)=
,
∴sinA=
,
∵0<A<
,∴A=
.
由正弦定理得
=
,又sinB=
,
∴AC=
=2,且sinC=
∴S△ABC=
|AC||BC|sinC=
.
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
则y=f(x)=2sin(x+
| π |
| 3 |
当x=2kπ+
| π |
| 6 |
(2)∵f(A-
| π |
| 3 |
| 3 |
∴2sin(A-
| π |
| 3 |
| π |
| 3 |
| 3 |
∴sinA=
| ||
| 2 |
∵0<A<
| π |
| 2 |
| π |
| 3 |
由正弦定理得
| BC |
| sinA |
| AC |
| sinB |
| ||
| 7 |
∴AC=
| BCsinB |
| sinA |
3
| ||
| 14 |
∴S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
点评:本题主要考察了三角函数中的恒等变换应用和正弦定理,属于中档题.

练习册系列答案
相关题目
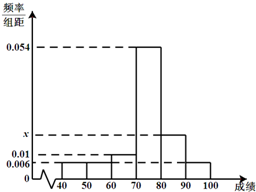 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]. 设圆(x-2)2+(y-2)2=4的切线l与两坐标轴交于点A(a,0),B(0,b),ab≠0.
设圆(x-2)2+(y-2)2=4的切线l与两坐标轴交于点A(a,0),B(0,b),ab≠0.