题目内容
2.判断下列复合命题的真假.(1)等腰三角形顶角的平分线平分底边并且垂直于底边;
(2)不等式x2-2x+1>0的解集为R且不等式x2-2x+2≤1的解集为∅.
分析 (1)根据复合命题分别进行判断即可.
(2)根据不等式的性质结合复合命题真假关系进行判断即可.
解答 解:(1)等腰三角形顶角的平分线平分底边并且垂直于底边为真命题;
(2)由x2-2x+1>0得(x-1)2>0,则当x=1时,不等式不成立,即不等式x2-2x+1>0的解集为R为假命题,
由等式x2-2x+2≤1得x2-2x+1≤0,即(x-1)2≤0,则x=1,故不等式x2-2x+2≤1的解集为∅是假命题,
则不等式x2-2x+1>0的解集为R且不等式x2-2x+2≤1的解集为∅为假命题.
点评 本题主要考查复合命题真假关系的判断,根据条件分别判断两个命题的真假是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
19.若函数f(x)=x3-6bx+3b在(0,1)内有极小值,则实数b的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (-∞,1) | C. | (0,+∞) | D. | (0,1) |
11.若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{4-2x>x-2}\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a≥-2 | B. | a<-2 | C. | a≤-2 | D. | a>-2 |
12.已知函数f(x)的导函数为f'(x),且满足f(x)=2xf'(1)+lnx,则$f'(\frac{1}{e})$=( )
| A. | $\frac{1}{e}-2$ | B. | e-2 | C. | -1 | D. | e |
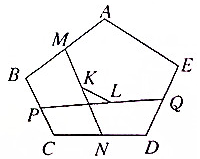 如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.
如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.