题目内容
12.已知等比数列{an}满足an+an+1=9•2n-1,n∈N*.(1)求数列{an}的通项公式;
(2)记bn=(-1)n$\frac{{9•{2^{n-1}}}}{{{a_n}{a_{n+1}}}}$,求数列{bn}的前n项和Tn;
(3)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对任意正整数n恒成立,求实数k的取值范围.
分析 (1){an}是等比数列,利用an+an+1=9•2n-1求出a1和q,可得数列{an}的通项公式.
(2)根据{an}是等比数列求出bn的通项公式,利用相消法可得数列{bn}的前n项和Tn;
(3)根据等比数列的前n项和公式求出Sn,由不等式Sn>kan-2对任意正整数n恒成立,分离参数k,转化为函数问题,利用单调性可得实数k的取值范围.
解答 解:(1)由题意,设等比数列{an}的公比为q,
∵an+an+1=9•2n-1,
令n=1,可得a1+a2=9…①
令n=2,可得a2+a3=18,即…②
由①②解得:q=2,a1=3.
∴等比数列{an}的通项公式为:${a}_{n}=3•{2}^{n-1}$.
(2)∵an+an+1=9•2n-1,bn=(-1)n$\frac{{9•{2^{n-1}}}}{{{a_n}{a_{n+1}}}}$,
∴bn=$\frac{{a}_{n}+{a}_{n+1}}{{a}_{n}{a}_{n+1}}$×(-1)n=$(-1)^{n}(\frac{1}{{a}_{n}}+\frac{1}{{a}_{n+1}})$
∴数列{bn}的前n项和Tn=$-(\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}})+(\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}})+$…+$(\frac{1}{{a}_{n}}+\frac{1}{{a}_{n+1}})×(-1)^{n}$=$-\frac{1}{{a}_{1}}+(-1)^{n}×\frac{1}{{a}_{n+1}}$
∵${a}_{n}=3•{2}^{n-1}$.
∴${a}_{n+1}=3•{2}^{n}$.
∴Tn=$\frac{1}{3}$$[\frac{(-1)^{n}}{{2}^{n}}-1]$
(3)由(1)知${S}_{n}=\frac{{{a}_{1}(q}^{n}-1)}{q-1}=3({2}^{n}-1)$
不等式Sn>kan-2,即3(2n-1)>k•3×2n-1-2对任意正整数n恒成立.
可得:$k<2-\frac{1}{3•{2}^{n-1}}$对任意正整数n恒成立.
令f(n)=$2-\frac{1}{3•{2}^{n-1}}$,
根据反比例的性质可知:f(n)随n的增大而增大.
∴当n=1时,f(n)取得最小值为$\frac{5}{3}$.
∴k$<\frac{5}{3}$.
故得实数k的取值范围是(-∞,$\frac{5}{3}$).
点评 本题主要考查数列通项公式和前n项和的求解,利用相消法求数列{bn}的前n项和是解决本题的关键,属于中档题.

| 日期 | 8月1日 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
| 平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
| 用电量(万度) | 38 | 35 | 41 | 36 | 30 |
(1)请根据表中的数据,求出y关于x的线性回归方程,据气象预报9月3日的平均气温是23℃,请预测9月3日的用电量;(结果保留整数)
(2)从表中任选两天,求用电量(万度)都超过35的概率.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.1 | 3.9 | 4.5 |
| A. | 8 | B. | 8.5 | C. | 9 | D. | 9.5 |
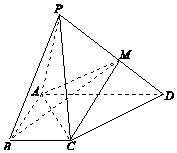 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠DAB=∠ABC=90°,AD=2BC,四棱锥P-ABCD的体积为10,点M在PD上.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠DAB=∠ABC=90°,AD=2BC,四棱锥P-ABCD的体积为10,点M在PD上.