题目内容
已知0<α<
<β<π,cos(α-β)=
,sinβ=
,则sinα=( )
| π |
| 2 |
| 4 |
| 5 |
| ||
| 10 |
A、
| ||||
B、±
| ||||
C、-
| ||||
D、-
|
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:先根据α和β的范围求得sin(α-β)和cosβ的值,进而利用正弦的两角和公式求得答案.
解答:
解:∵0<α<
<β<π,
∴-π<α-β<0,
∴sin(α-β)=-
=-
,cosβ=-
=-
,
∴sinα=sin(α-β+β)=-
×(-
)+
×
=
,
故选A.
| π |
| 2 |
∴-π<α-β<0,
∴sin(α-β)=-
1-
|
| 3 |
| 5 |
1-
|
3
| ||
| 10 |
∴sinα=sin(α-β+β)=-
| 3 |
| 5 |
3
| ||
| 10 |
| 4 |
| 5 |
| ||
| 10 |
13
| ||
| 50 |
故选A.
点评:本题主要考查了两角和与差的正弦函数.考查了学生对三角函数公式的灵活运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
一个正四棱锥的五个顶点都在半径为1的球面上,其中底面的四个顶点在该球的一个大圆上,则该正四棱锥的体积是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
(理)已知
=a,且函数 f(x)=aebx-cx有大于0的极点值,则实数b的取值范围是( )
| lim |
| x→2 |
| x2+cx+2 |
| x-2 |
| A、(-∞,-3) | ||
| B、(-3,+∞) | ||
C、(-∞,-
| ||
D、(-
|
一个算法的程序框图如图所示,若该程度输出的结果为
,则判断框①中应填入的条件是( )

| 7 |
| 12 |

| A、i<5 | B、i<4 |
| C、i>4 | D、i≤3 |
从装有4个红球和2个白球的口袋内任取3个球,那么互斥而不对立的两个事件是( )
| A、至少1个白球和都是红球 |
| B、恰有1个白球和都是红球 |
| C、至少1个白球和恰有1个红球 |
| D、至多1个白球和恰有1个红球 |
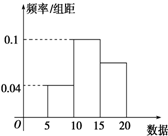 如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为( )
如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为( )| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
满足等式sinx=lgx的实数x的个数为( )
| A、1 | B、2 | C、3 | D、5 |
设函数f(x)=
,若f(a)<-1,则实数a的取值范围是( )
|
| A、(-∞,-1) |
| B、(-∞,-1)∪[0,2) |
| C、(2,+∞) |
| D、(-∞,-1)∪(2,+∞) |