题目内容
6.已知函数f(x)=sin(2x+φ)(φ∈R),且f(x)≤|f($\frac{π}{6}$)|,则f(x)图象的一条对称轴方程为( )| A. | x=$\frac{4π}{3}$ | B. | x=$\frac{2π}{3}$ | C. | x=$\frac{π}{2}$ | D. | x=-$\frac{π}{6}$ |
分析 先根据f(x)≤|f($\frac{π}{6}$)|,得到f($\frac{π}{6}$)为函数f(x)最大值或最小值,继而得到φ=kπ+$\frac{π}{6}$,k∈Z,由f(x)图象的对称轴方程为2x+φ=mπ+$\frac{π}{2}$,m∈Z,得到x=$\frac{1}{2}$(m-k)π+$\frac{π}{6}$,m,k∈Z,令m=2,k=1即可求出答案.
解答 解:f(x)≤|f($\frac{π}{6}$)|,
即f($\frac{π}{6}$)为函数f(x)最大值或最小值,
即2×$\frac{π}{6}$+φ=kπ+$\frac{π}{2}$,
∴φ=kπ+$\frac{π}{6}$,k∈Z,
∵f(x)图象的对称轴方程为2x+φ=mπ+$\frac{π}{2}$,m∈Z,
∴x=$\frac{mπ}{2}$+$\frac{π}{4}$-$\frac{1}{2}$(kπ+$\frac{π}{6}$)=$\frac{1}{2}$(m-k)π+$\frac{π}{6}$,m,k∈Z,
当m=2,k=1时,x=$\frac{2π}{3}$,
∴则f(x)图象的一条对称轴方程为x=$\frac{2π}{3}$,
故选:B
点评 本题考查了三角形函数的对称轴方程和三角形函数的最值问题,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
16.点P在直径为2的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| A. | $\frac{2\sqrt{70}}{5}$ | B. | $\frac{3\sqrt{70}}{5}$ | C. | $\frac{4\sqrt{15}}{5}$ | D. | $\frac{6\sqrt{15}}{5}$ |
14.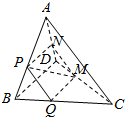 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )| A. | AC⊥BD | B. | AC∥截面PQMN | ||
| C. | AC=BD | D. | 异面直线PM与BD所成的角为45° |
11.两线段AB、CD不在同一平面内,如果AC=BD,AD=BC,则AB与CD( )
| A. | 垂直 | B. | 平行 | C. | 相交 | D. | 以上都不对 |
15.在△ABC中,已知cos(A-B)•cosB-sin(A-B)•sinB=0,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |