题目内容
14．
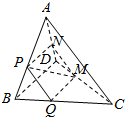如图，在四面体ABCD中，截面PQMN是正方形，且PQ∥AC，则下列命题中，错误的是（ ）| A． | AC⊥BD | B． | AC∥截面PQMN | ||
| C． | AC=BD | D． | 异面直线PM与BD所成的角为45° |
分析 首先由正方形中的线线平行推导线面平行，再利用线面平行推导线线平行，这样就把AC、BD平移到正方形内，即可利用平面图形知识做出判断．
解答 解：因为截面PQMN是正方形，所以PQ∥MN、QM∥PN，
则PQ∥平面ACD、QM∥平面BDA，
所以PQ∥AC，QM∥BD，
由PQ⊥QM可得AC⊥BD，故A正确；
由PQ∥AC可得AC∥截面PQMN，故B正确；
异面直线PM与BD所成的角等于PM与QM所成的角，故D正确；
综上C是错误的．
故选：C．
点评 本题主要考查线面平行的性质与判定，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
6．已知函数f（x）=sin（2x+φ）（φ∈R），且f（x）≤|f（$\frac{π}{6}$）|，则f（x）图象的一条对称轴方程为（ ）
| A． | x=$\frac{4π}{3}$ | B． | x=$\frac{2π}{3}$ | C． | x=$\frac{π}{2}$ | D． | x=-$\frac{π}{6}$ |
如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=PA，点O、D分别是AC、PC的中点，OP⊥平面ABC，