题目内容
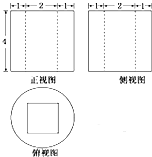
某几何体的三视图如图所示，则该几何体的体积是（ ）
| A、16π-16 |
| B、14π-16 |
| C、16π |
| D、18π-16 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知该几何体是一个底面半径为2，高为4的圆柱中间挖去一个底面边长为2，高为4的正四棱柱后剩下的部分，即可得出．
解答：
解：由三视图可知该几何体是一个底面半径为2，高为4的圆柱中间挖去一个底面边长为2，高为4的正四棱柱后剩下的部分，
所以其体积为π×22×4-22×4=16π-16．
故选：A．
所以其体积为π×22×4-22×4=16π-16．
故选：A．
点评：本题主要考查空间几何体的三视图及体积的求解．
练习册系列答案
春雨教育同步作文系列答案
相关题目
将函数y=3sin（2x-
）的图象向右平移
个单位长度，所得图象对应的函数（ ）
| π |
| 6 |
| π |
| 4 |
A、在区间[
| ||||
B、在区间[
| ||||
C、在区间[-
| ||||
D、在区间[-
|
已知y=
x3+bx2+（b+2）x+3是R上的单调增函数，则b的取值范围是（ ）
| 1 |
| 3 |
| A、-1＜b＜2 |
| B、-1≤b≤2 |
| C、b＜-1或b＞2 |
| D、b≤-2或b≥2 |