题目内容
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=3,AB=2,BC=
,则二面角P-BD-A的正切值为 .
| 3 |
考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:首先利用线面的垂直转化出二面角的平面角,进一步通过解直角三角形求得结果.
解答:
 解:四棱锥P-ABCD中,过点A做AE⊥BD
解:四棱锥P-ABCD中,过点A做AE⊥BD
由于:PA⊥平面ABCD,
所以:PA⊥BD
所以:BD⊥平面PAE
所以:∠PEA是二面角P-BD-A的平面角.
又PA=3,AB=2,BC=
,底面ABCD是矩形,
解得:AE=
所以:tan∠PEA=
=
故答案为:
 解:四棱锥P-ABCD中,过点A做AE⊥BD
解:四棱锥P-ABCD中,过点A做AE⊥BD由于:PA⊥平面ABCD,
所以:PA⊥BD
所以:BD⊥平面PAE
所以:∠PEA是二面角P-BD-A的平面角.
又PA=3,AB=2,BC=
| 3 |
解得:AE=
2
| ||
| 7 |
所以:tan∠PEA=
| AP |
| AE |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查的知识要点:线面垂直的判定和性质定理,二面角的平面角的应用.属于基础题型.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )
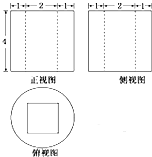

| A、16π-16 |
| B、14π-16 |
| C、16π |
| D、18π-16 |