题目内容
将函数y=3sin(2x-
)的图象向右平移
个单位长度,所得图象对应的函数( )
| π |
| 6 |
| π |
| 4 |
A、在区间[
| ||||
B、在区间[
| ||||
C、在区间[-
| ||||
D、在区间[-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,可得结论.
解答:
解:将函数y=3sin(2x-
)的图象向右平移
个单位长度,所得图象对应的函数为y=3sin[2(x-
)-
]=3sin(2x-
-
)=-sin(2x+
),
在区间[
,
]上,2x+
∈区间[
,
],y=-sin(2x+
)是增函数;
在区间[-
,
]上,2x+
∈区间[0,π],y=-sin(2x+
)不是增函数,也不是减函数,
故选:B.
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
在区间[
| π |
| 12 |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 3 |
在区间[-
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故选:B.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )
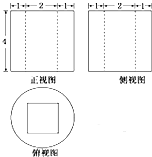

| A、16π-16 |
| B、14π-16 |
| C、16π |
| D、18π-16 |
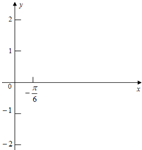 已知函数f(x)=2sin(2x-
已知函数f(x)=2sin(2x-