题目内容
设m∈R,在平面直角坐标系中,已知向量
=(mx,y+1),向量
=(x,y-1),
⊥
,动点M(x,y)的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)当m=
时,轨迹E与直线y=x-1交于A、B两点,求弦AB的长.
| a |
| b |
| a |
| b |
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)当m=
| 1 |
| 4 |
考点:曲线与方程
专题:圆锥曲线的定义、性质与方程
分析:(1)直接由两向量的数量积为0列式求得轨迹E的方程,然后根据m的范围说明曲线的形状;
(2)把m=
代入轨迹方程,联立直线方程和椭圆方程,求得两交点的坐标,由两点间的距离公式得答案.
(2)把m=
| 1 |
| 4 |
解答:
解:(1)∵
=(mx,y+1),
=(x,y-1),且
⊥
,
∴
•
=mx2+y2-1=0,即mx2+y2=1.
当m=0时,方程表示两直线,方程为y=±1;
当m=1时,方程表示的是圆x2+y2=1;
当m>0且m≠1时,方程表示的是椭圆;
当m<0时,方程表示的是双曲线;
(2)当m=
时,椭圆方程为
+y2=1.
设A(x1,y1),B(x2,y2),
联立
,得5x2-8x=0,
解得:x1=0,x2=
.
∴y1=-1,y2=
.
∴A(0,-1),B(
,
),
则|AB|=
=
.
| a |
| b |
| a |
| b |
∴
| a |
| b |
当m=0时,方程表示两直线,方程为y=±1;
当m=1时,方程表示的是圆x2+y2=1;
当m>0且m≠1时,方程表示的是椭圆;
当m<0时,方程表示的是双曲线;
(2)当m=
| 1 |
| 4 |
| x2 |
| 4 |
设A(x1,y1),B(x2,y2),
联立
|
解得:x1=0,x2=
| 8 |
| 5 |
∴y1=-1,y2=
| 3 |
| 5 |
∴A(0,-1),B(
| 8 |
| 5 |
| 3 |
| 5 |
则|AB|=
(
|
| 8 |
| 5 |
| 2 |
点评:本题考查了平面向量的数量积运算,考查了轨迹方程的求法,考查了两点间的距离公式,是中档题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )
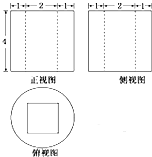

| A、16π-16 |
| B、14π-16 |
| C、16π |
| D、18π-16 |
圆x2+y2+2x-6y-15=0与直线(1+3m)x+(3-2m)y+4m-17=0的交点个数是( )
| A、2 | B、1 | C、0 | D、与m有关 |