题目内容
已知y=
x3+bx2+(b+2)x+3是R上的单调增函数,则b的取值范围是( )
| 1 |
| 3 |
| A、-1<b<2 |
| B、-1≤b≤2 |
| C、b<-1或b>2 |
| D、b≤-2或b≥2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:利用三次函数y=
x3+bx2+(b+2)x+3的单调性,通过其导数进行研究,求出导数,利用其导数恒大于0即可解决问题.
| 1 |
| 3 |
解答:
解:∵已知y=
x3+bx2+(b+2)x+3
∴y′=x2+2bx+b+2,
∵函数是R上的单调增函数,
∴x2+2bx+b+2≥0恒成立,
∴△≤0,即b2-b-2≤0,
则b的取值是-1≤b≤2.
故选:B.
| 1 |
| 3 |
∴y′=x2+2bx+b+2,
∵函数是R上的单调增函数,
∴x2+2bx+b+2≥0恒成立,
∴△≤0,即b2-b-2≤0,
则b的取值是-1≤b≤2.
故选:B.
点评:本题考查函数的单调性及单调区间、利用导数解决含有参数的单调性问题,考查转化思想以及计算能力.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
平面直角坐标系中,双曲线方程
-
=1(m,n>0),A,C是双曲线的两焦点,B是双曲线上的点,在△ABC中,|
|=
,则双曲线的离心率为( )
| x2 |
| m2 |
| y2 |
| n2 |
| sinA-sinB |
| sinC |
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
某几何体的三视图如图所示,则该几何体的体积是( )
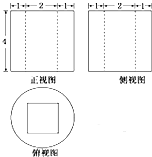

| A、16π-16 |
| B、14π-16 |
| C、16π |
| D、18π-16 |
空间直角坐标系中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、无法确定 |
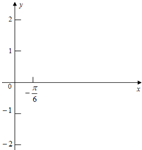 已知函数f(x)=2sin(2x-
已知函数f(x)=2sin(2x-