题目内容
2.已知曲线y=lnx的切线过原点,则此切线的斜率是$\frac{1}{e}$.分析 设切点坐标为(a,lna),求函数的导数,可得切线的斜率,切线的方程,代入(0,0),求切点坐标,切线的斜率.
解答 解:设切点坐标为(a,lna),
∵y=lnx,∴y′=$\frac{1}{x}$,
切线的斜率是$\frac{1}{a}$,
切线的方程为y-lna=$\frac{1}{a}$(x-a),
将(0,0)代入可得lna=1,∴a=e,
∴切线的斜率是$\frac{1}{a}$=$\frac{1}{e}$.
故答案为:$\frac{1}{e}$.
点评 本题主要考查导数的几何意义,利用切线斜率和导数之间的关系可以求切点坐标是解题的关键,考查运算能力,属于基础题.

练习册系列答案
相关题目
13.已知函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0),f(x)在区间(0,2]上只有一个最大值1和一个最小值-1,则实数ω的取值范围为( )
| A. | [$\frac{7π}{12}$,$\frac{13π}{12}$) | B. | [$\frac{π}{2}$,π) | C. | [$\frac{π}{6}$,$\frac{π}{2}$) | D. | [$\frac{π}{6}$,$\frac{π}{3}$] |
11.若$\overrightarrow{a}$=(cos20°,sin20°),$\overrightarrow{b}$=(cos10°,sin190°),则$\overrightarrow{a}$•$\overrightarrow{b}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | cos10° | D. | $\frac{\sqrt{2}}{2}$ |
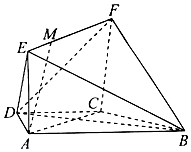 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. 某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.
某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.