题目内容
11．若$\overrightarrow{a}$=（cos20°，sin20°），$\overrightarrow{b}$=（cos10°，sin190°），则$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | cos10° | D． | $\frac{\sqrt{2}}{2}$ |
分析 进行数量积的坐标运算，并根据两角差的余弦公式化简即可得出$\overrightarrow{a}•\overrightarrow{b}=cos30°$，从而找出正确选项．
解答 解：$\overrightarrow{a}•\overrightarrow{b}=cos20°cos10°+sin20°sin190°$
=cos20°cos10°-sin20°sin10°
=cos（20°+10°）
=$\frac{\sqrt{3}}{2}$．
故选B．
点评 考查数量积的坐标运算，两角差的余弦公式，以及三角函数的诱导公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．执行如图所示的程序框图，如果输入s=0.1，则输出的n=（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
6．执行如图所示的程序框图，则输出S=（ ）
| A． | 4 | B． | log215 | C． | log217 | D． | 3 |
3．
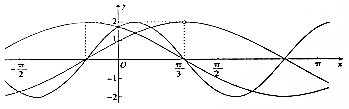已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）
已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）| A． | x=$\frac{π}{6}$ | B． | x=$\frac{13π}{6}$ | C． | x=-$\frac{23π}{12}$ | D． | x=-$\frac{29π}{12}$ |