题目内容
13.已知函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0),f(x)在区间(0,2]上只有一个最大值1和一个最小值-1,则实数ω的取值范围为( )| A. | [$\frac{7π}{12}$,$\frac{13π}{12}$) | B. | [$\frac{π}{2}$,π) | C. | [$\frac{π}{6}$,$\frac{π}{2}$) | D. | [$\frac{π}{6}$,$\frac{π}{3}$] |
分析 根据函数f(x)的解析式,利用x的取值范围与三角函数图象与性质,列出不等式求出ω的取值范围.
解答 解:函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0),
当x∈(0,2]时,$\frac{π}{3}$<ωx+$\frac{π}{3}$≤2ω+$\frac{π}{3}$;
又函数f(x)在区间(0,2]上只有一个最大值1和一个最小值-1,
∴$\frac{3π}{2}$≤2ω+$\frac{π}{3}$<$\frac{5π}{2}$,
解得$\frac{7π}{12}$≤ω<$\frac{13π}{12}$,
∴实数ω的取值范围是[$\frac{7π}{12}$,$\frac{13π}{12}$).
故选:A.
点评 本题考查了正弦型函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
1.执行如图所示的程序框图,如果输入s=0.1,则输出的n=( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.某单位生产A、B两种产品,需要资金和场地,生产每吨A种产品和生产每吨B种产品所需资金和场地的数据如表所示:
现有资金12万元,场地400平方米,生产每吨A种产品可获利润3万元;生产每吨B种产品可获利润2万元,分别用x,y表示计划生产A、B两种产品的吨数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 3 | 50 |
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
5.已知a∈{-2,0,1,3},b∈{1,2},则曲线ax2+by2=1为椭圆的概率是( )
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
3.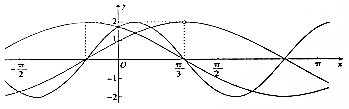 已知ω>0,a>0,f(x)=asinωx+$\sqrt{3}$acosωx,g(x)=2cos(ax+$\frac{π}{6}$),h(x)=$\frac{f(x)}{g(x)}$这3个函数在同一直角坐标系中的部分图象如图所示,则函数g(x)+h(x)的图象的一条对称轴方程可以为( )
已知ω>0,a>0,f(x)=asinωx+$\sqrt{3}$acosωx,g(x)=2cos(ax+$\frac{π}{6}$),h(x)=$\frac{f(x)}{g(x)}$这3个函数在同一直角坐标系中的部分图象如图所示,则函数g(x)+h(x)的图象的一条对称轴方程可以为( )
 已知ω>0,a>0,f(x)=asinωx+$\sqrt{3}$acosωx,g(x)=2cos(ax+$\frac{π}{6}$),h(x)=$\frac{f(x)}{g(x)}$这3个函数在同一直角坐标系中的部分图象如图所示,则函数g(x)+h(x)的图象的一条对称轴方程可以为( )
已知ω>0,a>0,f(x)=asinωx+$\sqrt{3}$acosωx,g(x)=2cos(ax+$\frac{π}{6}$),h(x)=$\frac{f(x)}{g(x)}$这3个函数在同一直角坐标系中的部分图象如图所示,则函数g(x)+h(x)的图象的一条对称轴方程可以为( )| A. | x=$\frac{π}{6}$ | B. | x=$\frac{13π}{6}$ | C. | x=-$\frac{23π}{12}$ | D. | x=-$\frac{29π}{12}$ |