题目内容
17.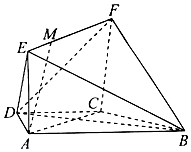 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.(I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.
分析 (Ⅰ)由已知,若证得AC⊥BC,则据面面垂直的性质定理即可.转化成在平面ABCD,能否有AC⊥BC,易证成立.
(Ⅱ)设AC∩BD=N,则面AMF∩平面BDF=FN,只需AM∥FN即可.而CN:NA=1:2.故应有EM:FM=1:2
解答 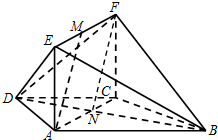 (Ⅰ)证明:在梯形ABCD中,
(Ⅰ)证明:在梯形ABCD中,
∵AD=DC=CB=a,∠ABC=60°
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=90°,∴AC⊥BC,
又∵平面ACF⊥平面ABCD,交线为AC,∴BC⊥平面ACFE.
(Ⅱ)当EM=$\frac{\sqrt{3}}{3}$a时,AM∥平面BDF.
在梯形ABCD中,设AC∩BD=N,连接FN,则CN:NA=1:2.
∵EM=$\frac{\sqrt{3}}{3}$a而EF=AC=$\sqrt{3}$a,∴EM:FM=1:2.∴EM∥CN,EM=CN,
∴四边形ANFM是平行四边形.∴AM∥NF.
又NF?平面BDF,AM?平面BDF.∴AM∥平面BDF.
点评 本题考查线面位置关系及判定,考查空间想象能力,计算能力,转化能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.某单位生产A、B两种产品,需要资金和场地,生产每吨A种产品和生产每吨B种产品所需资金和场地的数据如表所示:
现有资金12万元,场地400平方米,生产每吨A种产品可获利润3万元;生产每吨B种产品可获利润2万元,分别用x,y表示计划生产A、B两种产品的吨数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 3 | 50 |
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
5.已知a∈{-2,0,1,3},b∈{1,2},则曲线ax2+by2=1为椭圆的概率是( )
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
6.执行如图所示的程序框图,则输出S=( )


| A. | 4 | B. | log215 | C. | log217 | D. | 3 |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,以F1F2为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |