题目内容
12．
某年级480名学生在一次面米测试中，成绩全部介于13秒和18秒之间，将测试结果分成5组，如图为其频率分布直方图，如果从左到右的5个小矩形的面积之比为1：3：7：6：3，那么成绩在[16，18]的学生人数是216．
分析 先求出成绩在[16，18]的学生的频率，由此能求出成绩在[16，18]的学生人数．
解答 解：频率分布直方图中，
从左到右的5个小矩形的面积之比为1：3：7：6：3，
∴成绩在[16，18]的学生的频率为：$\frac{6+3}{1+3+7+6+3}$=0.45，
∴成绩在[16，18]的学生人数是：480×0.45=216．
故答案为：216．
点评 本题考查频数的求法，是基础题，解题时要认真审题，注意频率分布直方图的性质的合理运用．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
3．
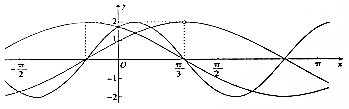已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）
已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）| A． | x=$\frac{π}{6}$ | B． | x=$\frac{13π}{6}$ | C． | x=-$\frac{23π}{12}$ | D． | x=-$\frac{29π}{12}$ |
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，以F1F2为直径的圆与双曲线渐近线的一个交点为（3，4），则此双曲线的方程为（ ）
| A． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B． | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | C． | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |