题目内容
14．已知函数y=x2+$\frac{a}{x}$（a∈R）在x=1处的切线与直线2x-y+1=0平行，则a=（ ）| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
分析 求函数的导数，利用导数的几何意义，以及两直线平行的条件：斜率相等，建立方程关系，解方程即可得到a的值．
解答 解：∵函数y=x2+$\frac{a}{x}$（a∈R）在x=1处的切线与直线2x-y+1=0平行，
∴f′（1）=2，
由f′（x）=2x-$\frac{a}{{x}^{2}}$，
即f′（1）=2-a=2，解得a=0，
故选：A．
点评 本题主要考查导数的几何意义，根据导数和切线斜率之间的关系是解决本题的关键，比较基础．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
5．已知a∈{-2，0，1，3}，b∈{1，2}，则曲线ax2+by2=1为椭圆的概率是（ ）
| A． | $\frac{3}{7}$ | B． | $\frac{4}{7}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{8}$ |
6．执行如图所示的程序框图，则输出S=（ ）
| A． | 4 | B． | log215 | C． | log217 | D． | 3 |
3．
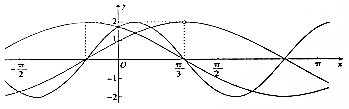已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）
已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）| A． | x=$\frac{π}{6}$ | B． | x=$\frac{13π}{6}$ | C． | x=-$\frac{23π}{12}$ | D． | x=-$\frac{29π}{12}$ |